Droite remarquable d'un triangle
-
Joyca Le Boss dernière édition par Joyca Le Boss
Bonjour je n'ai pas compris cet exercice pouvez vous m'aider a le resoudre svp?
consigne ;
Si A :(-3 ;7), B :(3 ;-5) donner l’équation de l’ensemble des points P tels que la distance à A est double de celle à B
-
mtschoon dernière édition par mtschoon

@Joyca-Le-Boss , bonjour,
Piste pour démarrrer,
PA=2PBPA=2PBPA=2PB
Soit (x,y) les coordonnées de P
(xA−xP)2+(yA−yP)2=2(xB−xP)2+(yB−yP)2\sqrt{(x_A-x_P)^2+(y_A-y_P)^2}=2\sqrt{(x_B-x_P)^2+(y_B-y_P)^2}(xA−xP)2+(yA−yP)2=2(xB−xP)2+(yB−yP)2
Tu remplaces par les valeurs données, puis tu élèves au carré.
-
mtschoon dernière édition par

Tu dois obtenir :
(−3−x)2+(7−y)2=2(3−x)2+(−5−y)2\sqrt{(-3-x)^2+(7-y)^2}=2\sqrt{(3-x)^2+(-5-y)^2}(−3−x)2+(7−y)2=2(3−x)2+(−5−y)2Après élévation au carré et transposition dans le membre de gauche, sauf erreur, tu dois obtenir :
−3x2+30x−3y2−54y−78=0-3x^2+30x-3y^2-54y-78=0−3x2+30x−3y2−54y−78=0
En divisant par −3-3−3 , tu dois reconnaître l'équation d'un cercle.
-
Joyca Le Boss dernière édition par
@mtschoon J'ai compris! merci de votre aide!
-
mtschoon dernière édition par mtschoon

@Joyca-Le-Boss , de rien.
Je pense que tu as trouvé :
x2+y2−10x+18y+26=0x^2+y^2-10x+18y+26=0x2+y2−10x+18y+26=0
Après transformation :
(x−5)2+(y+9)2=80(x-5)^2+(y+9)^2=80(x−5)2+(y+9)2=80
L'ensemble des points P est le cercle de centre I(5,−9)I(5,-9)I(5,−9) et de rayon R=80=45R=\sqrt 80=4\sqrt 5R=80=45
-
mtschoon dernière édition par

Illustration graphique :
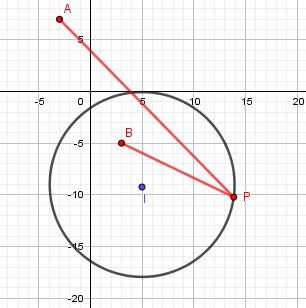
-
mtschoon dernière édition par mtschoon

@Joyca-Le-Boss , une remarque :
Ton titre est bizarre car il ne s'agit pas d'une droite remarquable,(et encore moins dans un triangle) mais d'un cercle.
Tu aurais trouvé une droite remarquable ( médiatrice) si tu avais cherché l'ensemble des points P tels que la distance à A est égale à la distance à B :
PA=PBPA=PBPA=PB <=> P∈ΔP \in \DeltaP∈Δ, avec(Δ(\Delta(Δ médiatrice de [AB] )