Devoir de maison sur les vecteurs
-
Wil Fried dernière édition par

Bonsoir, aidez moi svp!
Soit ( O,i,j ) un repère. On donne A(2;-3), B(-3;2) et C(3,2)
1-a) Calcule les coordonnées du point A′A'A′ milieu de [BC][BC][BC].
Je trouve A'(0;2)
1-b) Calcule les coordonnées de G tel que GA′→\overrightarrow{GA'}GA′ = 13\frac{1}{3}31AA′→\overrightarrow{AA'}AA′. Dis ce que représente G pour le triangle ABCABCABC.
-
@Wil-Fried Bonsoir,
Si G(x;y)G(x;y)G(x;y) ;
GA′→=(0−x;2−y)\overrightarrow{GA'}=(0-x;2-y)GA′=(0−x;2−y)
calcule les coordonnées du vecteur AA′→\overrightarrow{AA'}AA′, puis en utilisant la relation, tu calcules les coordonnées point GGG.
-
mtschoon dernière édition par mtschoon

Bonsoir,
@Wil-Fried , oui pour les coordonnées de A'
Si tu le souhaites, tu peux calculer les coordonnées de G en résolvant directement les équations :
xA′−xGx_A'-x_GxA′−xG=13(xA′−xA)\dfrac{1}{3}(x_A'-x_A)31(xA′−xA)
yA′−yGy_A'-y_GyA′−yG=13(yA′−yA)\dfrac{1}{3}(y_A'-y_A)31(yA′−yA)Sauf erreur, tu dois trouver G(23,13)G(\dfrac{2}{3},\dfrac{1}{3})G(32,31)
Pour la propriété de G, tu peux éventuellemnt consulter ici :http://cedric.beltrami.free.fr/mediane.html
-
Wil Fried dernière édition par

@mtschoon Les coordonnées de G sont plutôt 2/3 et 1/3
-
Wil Fried dernière édition par

@mtschoon 1-) Vérifier que GA+GB+GC=0. J'ai bien vérifié et je trouve 0.
2) Calculer la longueur OA, OB et OC.
Je trouve une valeur de 11\sqrt{11}11 pour les trois longueurs.
Que représente O pour le triangle ABC ?
Je répond que O est le centre du cercle circonscrit au triangle ABC.
3-a) Calcule les coordonnées de H tel que ( vecteur sur tout ce qui suit) : OH=OA+OB+OC
Je trouve H( 2;1)
3-b) Montrer que (vecteurs) OH=2OA
J'arrive pas.
3-c) Déduis-en que (AH) et (BC) sont perpendiculaires.
3-d) Détermine le nombre réel k tel que(vecteurs) OH=k×OG
4) Déduis-en que les points O, G et H sont alignés.
Voici les questions auxquelles j'arrive pas à répondre.
-
Oui pour les coordonnées du point G.
- Juste
- Refais le calcul 22+(−3)2=...2^2+(-3)^2= ...22+(−3)2=...
3- a) Juste
3 -b) Vérifie l'énoncé.
-
mtschoon dernière édition par mtschoon

Bonjour,
Oui @Wil-Fried , c'est bien (23,13)(\dfrac{2}{3},\dfrac{1}{3})(32,31) pour G
Pour la 2) tu as dû trouver, après rectification, que le rayon du cercle circonscrit au triangle ABC est 13\sqrt{13}13
H(2,1)H(2,1)H(2,1) est bon pour la 3)a), comme déjà indiqué.
Pour que la suite et fin de l'exercice soit cohérentes (droite d'EULER du triangle) il faudrait montrer pour la 3)b) que :
AH→=2OA′→\overrightarrow{AH}=2\overrightarrow{OA'}AH=2OA′ (à vérifier)Je joins un schéma ci besoin
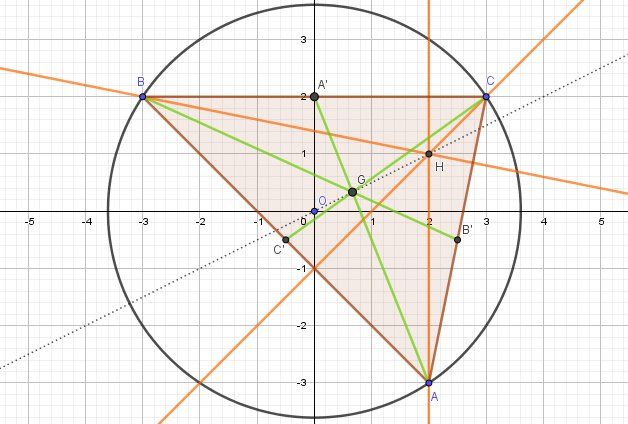
-
Wil Fried dernière édition par

@Noemi Merci beaucoup
-
Wil Fried dernière édition par

@mtschoon La représentation m'a aidé. Merci beaucoup
-
mtschoon dernière édition par

De rien @Wil-Fried
J'espère que m proposition pour la 3)b) est bien celle de ton énoncé.
-
Wil Fried dernière édition par

@mtschoon C'est bien cela. J'avais fais une erreur dans l'écriture..
-
mtschoon dernière édition par

@Wil-Fried , c'est parfait.
Comme tu as dû conclure, les points O (centre du cercle circonscrit au triangle-intersection des médiatrices), G (centre de gravité-intersection des médianes), H (orthocentre-intersection des hauteurs) sont alignés sur la droite appelée droite d'Euler du triangle.
-
Wil Fried dernière édition par

@mtschoon Merci pour la conclusion. Merci pour la conclusion. Ma conclusion n'était pas top!
-
mtschoon dernière édition par

C'est bien si tout est maintenant clair pour toi.