Nombres complexes et similitudes

[Lili Cc]

Bonsoir, je suis entrain de traiter un exercice sur les nombres complexes et on demande de déterminer la nature et les éléments caractéristiques de f.
f : z'= (⅗+⅘i)z(barre) + i.
J'ai trouvé |a|=1 donc c'est soit une symétrie glissée soit une symétrie orthogonale. Mais je ne sais pas comment faire pour la suite.

[Noemi]

@Lili-Cc Bonsoir,

$f$ est une similitude plane inverse de rapport 1.
Cherche les coordonnées du centre de la similitude, soit les coordonnées du point invariant en posant $z^{\prime }=z$.

[mtschoon]

Bonjour

@Noemi a dit dans Nombres complexes et similitudes :

@Lili-Cc Bonsoir,

$f$ est une similitude plane inverse de rapport 1.
Cherche les coordonnées du centre de la similitude, soit les coordonnées du point invariant en posant $z^{\prime }=z$.

@Lili-Cc , je revois cela,

f définie par :
$\boxed{z^{\prime }=(\frac{3}{5}+\frac{4}{5}i)\bar{z}+i}$ de la forme $\boxed{z^{\prime }=a\bar{z}+b}$

cette transformation fait partie des isométries, et en particulier , il s'agit d'un anti-déplacement.

Comme tu l'as indiqué, $|a|=1$

Après calcul, sauf erreur, $a\bar{b}+b=\frac{4}{5}+\frac{2}{5}i$

$a\bar{b}+b\ne 0$ . Il s'agit d'une symétrie glissée, composée d"une translation et d'une symétrie orthogonale axiale ( on dit aussi réflexion au lieu de symétrie orthogonale axiale )

Pas de point invariant.

Pour $z=0$, $z^{\prime }=i$
Image du point $O$ par f est le point $O^{\prime }(0,1)$
Soit I le milieu de $[O,O^{\prime }]$
$I$ a pour coordonnées $(0,\frac{1}{2})$

Après calculs, l'image de $O$ par $fof$ est $O^{\prime \prime }$ de coordonnées $(\frac{4}{5},\frac{2}{5})$

$\frac{1}{2}\overrightarrow{O{O}^{\prime \prime }}$ a pour coordonnées $(\frac{2}{5},\frac{1}{5})$

Tu appliques ton cours :
f est la composée de la translation $T_{\overrightarrow{U}}$ (avec $\overrightarrow{U}=\frac{1}{2}\overrightarrow{O{O}^{\prime \prime }}$) et de la symétrie axiale $S_{\Delta }$ (avec $\Delta$ droite passant par $I$ et dirigée par $\overrightarrow{U})$

$\boxed{f=T_{\overrightarrow{U}}o{S}_{\Delta }=S_{\Delta }o{T}_{\overrightarrow{U}}}$

[mtschoon]

@Lili-Cc , je te mets une schéma.

L'image de M par $T_{\overrightarrow{U}}$ est $M^{\prime }$
L'image de $M^{\prime }$ par $S_{\Delta }$ est $M^{\prime \prime }$
Donc
L'image de $M$ par f est $M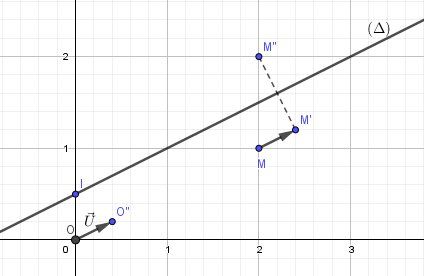^{\prime \prime }$

Remarque : pour pouvoir faire une vérification de tes calculs, j'ai pris des valeurs simples dans le graphique :
$M(2,1)$
L'image de M par f est $M^{\prime \prime }(2.2)$

[mtschoon]

@Lili-Cc , si ton cours n'est pas clair, tu peux regarder ici, paragraphe 6.4
http://mdevmd.accesmad.org/mediatek/pluginfile.php/2378/mod_resource/content/6/Isometries et nombres complexes - coursTC_TD - accesmad.htm