Proportionnalité : Longueur d'un cercle et périmètre d'un carré
-
EEnzo Hochart dernière édition par Noemi
Bonjour, jai un exercice que je n'arrive a faire il est très urgent pouvez vous le faire? Merci.
Y a-t-il proportionnalité entre la longueur du cercle et le périmètre du carré inscrit dans ce cercle justifier la réponse ? (L'image c'est un carré dans un cercle)
-
@Enzo-Hochart Bonsoir,
Désolée, je ne fais pas les exercices, je fournis juste des pistes.
Le périmètre du cercle : p=2πRp= 2\pi Rp=2πR
et le périmètre du carré :....
Calcule la mesure du côté du carré en utilisant le théorème de Pythagore ;
c2=R2+R2c^2= R^2+R^2c2=R2+R2, c=....c = ....c=....
-
mtschoon dernière édition par mtschoon

Bonjour,
@Enzo-Hochart , ici , effectivement les scans d'énoncés ne sont pas autorisés, mais ils sont autorisés pour les graphiques.
Tu aurais dû mettre l'image pour éclairer l'exercice.
J'en joins une
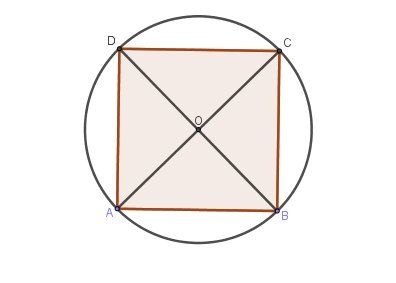
Un conseil : n'attends pas le dernier moment pour faire ton travail ou demander de l'aide ; travailler dans l'urgence (et demander qu'on te fasse l'exercice ! ) ne te fera pas progresser.
En appelant RRR le rayon du cercle, tu sais déjà que le périmètre du cercle est 2πR2\pi R2πR
Les diagonales d'un carré sont perpendiculaires.
Avec les notations que j'ai utilisées dans mon graphique, en utilisant le triangle rectangle AOB
AB2=OA2+OB2=......=2R2AB^2=OA^2+OB^2=......=2R^2AB2=OA2+OB2=......=2R2
AB=R2AB=R\sqrt 2AB=R2
Le périmètre du carré est donc 4R24R\sqrt 24R2Il te reste à savoir s'il existe un nombre réel kkk fixé, tel que :
2πR=k(4R2)2\pi R=k(4R\sqrt 2)2πR=k(4R2)Donne ta réponse si tu souhaites une vérification.