Equation cercle coordonnées point intersection

@Joyca-Le-Boss
3)L’équation suivante est-elle celle d’un cercle ?
𝑥²+𝑦²−4𝑥+9𝑦−5=0
Si oui, précise son centre, son rayon et donne l’équation explicite de celui-ci

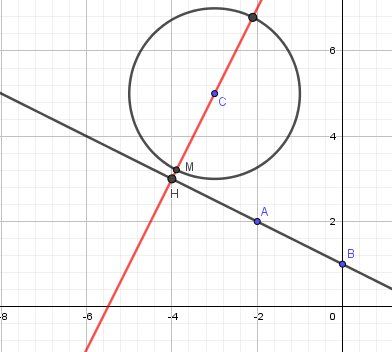
Détermine la coordonnée des éventuels points d’intersection entre le cercle de centre C :(-3,5) et de rayon 2 et la droite passant par les points A :(0,1) et B :(-2,2).
En utilisant la réciproque du théorème de Pythagore, déterminer l’ordonnée du point C d’abscisse -2 tel que le triangle ABC soit rectangle en A si A :(1,-4) et B :(-2,5)

@Joyca-Le-Boss

Ces questions ont été déplacées pour alléger le post.
Question 3, Il faut écrire l'équation sous la forme : $x-a)^2+(y-b)^2=R^2$
$(x−2)2−4+(y+92)2−814−5=0(x-2)^2-4+(y+\dfrac{9}{2})^2-\dfrac{81}{4}-5= 0$
....
Je te laisse poursuivre

Bonjour

@Joyca Le Boss, Je t'avais conseillé sur ce topic joint où tu avais posté un exercice avec 7 questions, de séparer les questions pour éviter un topic trop long.
Il aurait fallu le faire maintenant...

https://forum.mathforu.com/topic/32299/les-équations-de-la-droites-parallélisme-et-perpendicularité/3

Pour la question 3), je pense que tu as trouvé qu'il s'agit du cercle de centre $I(2,−92)I(2,-\dfrac{9}{2})$ et de rayon $R=1172R=\dfrac{\sqrt{117}}{2}$

Piste pour la question 4)

Equation du cercle (E) de de centre $C (- 3, 5)$ et de rayon $2$ :
$x+3)^2+(y-5)^2=4$

Tu peux éventuellement développer et transposer et obtenir :
$x^2+y^2+6x-10y+30=0$

Equation de la droite (D) passant par les points A (0,1) et B (-2,2).

Je t'ai donné une méthode (il y en a d'autres) dans l'exercice du lien joint (question b).
Donc, tu dois savoir faire (relis la réponse éventuellement).
Tu dois trouver, sauf erreur :
$y=−12x+1y=-\dfrac{1}{2}x+1$

Pour étudier l'intersection de (E) avec (D), tu résous de système composé des équations de (E) avec (D)

${x2+y2+6x−10y+30=0y=−12x+1\begin{cases}x^2+y^2+6x-10y+30=0\cr y=-\dfrac{1}{2}x+1\end{cases}$

Tu peux résoudre par substitution en remplaçant $y$ par $−12x+1-\dfrac{1}{2}x+1$ dans la première équation.
Tu obtiendras ainsi une équation du second degré d'inconnue $x$
Pour résoudre, en calculant le discriminant $Δ\Delta$ , sauf erreur, tu trouveras $Δ\Delta$ strictement négatif, donc équation impossible.

Conclusion : il n'y a pas de points d'intersection entre (E) et (D) (ce qui justifie le terme "éventuellement" de la question.)

Illustration graphique :

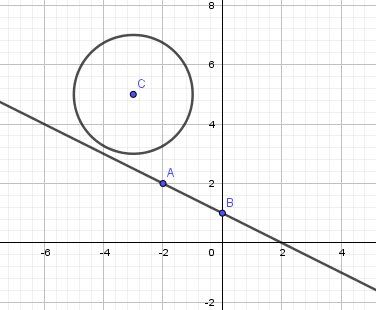
Remarque : au lieu de passer par le système d'équations, si tu connais (?) la formule donnant la distance $d$ d'un point à une droite, tu peux trouver que la distance du point $C$ à la droite $(D)$ est strictement supérieure à 2, d'où : pas de point d'intersection.

Revois tout ça et passe à la question 5).

@Joyca-Le-Boss ,

Autre façon (beaucoup plus rapide ! ) pour répondre à la 4) en connaissant la formule donnant la distance $d$ d'un point de coordonnées ( $x_0,y_0$ ) à une droite (D) d'équation $a x + b y + c = 0$ (avec $(a,b)≠(0,0))(a,b)\ne (0,0))$ , en repère orthonormé bien sûr .

$d=∣ax0+by0+c∣a2+b2\boxed{d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}}$

Dans ta question : $C (- 3, 5)$ donc $x_0=-3$ et $y_0=5$

La droite passant par A et B :
$y=−12x+1y=-\dfrac{1}{2}x+1$ <=> $y+12x−1=0y+\dfrac{1}{2}x-1=0$

En multipliant par 2 pour faire plus simple : $x + 2 y - 2 = 0$

on prend $a = 1$ et $b = 2$

$d=∣−3+2(5)−2∣12+22=55=5d=\dfrac{|-3+2(5)-2|}{\sqrt{1^2+2^2}}=\dfrac{5}{\sqrt 5}=\sqrt 5$

$5≈2.236\sqrt 5\approx 2.236$ donc $5>2\sqrt 5\gt 2$ c'est à dire $d>R\boxed{d\gt R}$

La distance du point C à la droite (AB) étant strictement supérieure au rayon du cercle , la droite ne peut pas rencontrer le cercle.

Cette méthode évite de chercher l'équation du cercle et de résoudre le système "cercle-droite", mais évidemment , tu ne peux l'utiliser que si cette formule figure dans ton cours...

Illustration graphique

$C M = 2$
$CH=5CH=\sqrt 5$