Fonctions réciproques
-
JJbuilder dernière édition par
Salut !
J’ai un souci avec la question suivante dans mon exercice :
Soit la fonction f(x)=√4x+3f(x)=√4x+3 f(x)=√4x+3
Explicite la fonction réciproque f−1f^-1f−1 de la fonction fff
Voici ce que j’obtiens : y=√4x+3y=√4x+3y=√4x+3 <=> y2=4x+3y^2=4x+3y2=4x+3 <=> y2−3=4xy^2-3=4xy2−3=4x <=> x=y2−3/4x=y^2-3/4x=y2−3/4 donc f−1(x)=x2−3/4f^-1(x)=x^2-3/4f−1(x)=x2−3/4 ma préoccupation est de savoir si ma démarche est juste et sinon aidez-moi s’il vous plaît à résoudre le problème. Merci d’avance
-
@Jbuilder Bonjour,
Il manque le domaine de validité et des parenthèses à l'expression finale (x2−3)4\dfrac{(x^2-3)}{4}4(x2−3).
-
JJbuilder dernière édition par
@Noemi
Encore une fois merci je ne sais pas comment vous remercier
-
L'essentiel c'est que tu comprennes les résolutions et que tu sois capable de les appliquer lors des évaluations.
-
mtschoon dernière édition par

Bonjour,
Effectivement, les ensembles de validité ne sont pas indiqués...ce qui est indispensable.
fff, définie par f(x)=4x+3f(x)=\sqrt{4x+3}f(x)=4x+3, est une bijection de [−34,+∞[[\dfrac{-3}{4},+\infty[[4−3,+∞[ vers [0,+∞[[0,+\infty[[0,+∞[
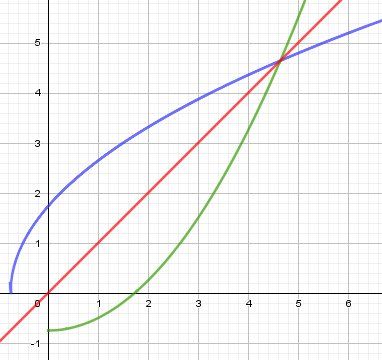
f−1f^{-1}f−1, définie par f−1(x)=x2−34f^{-1}(x)=\dfrac{x^2-3}{4}f−1(x)=4x2−3, est une bijection de [0,+∞[[0,+\infty[[0,+∞[, vers [−34,+∞[[\dfrac{-3}{4},+\infty[[4−3,+∞[Représentation graphique . en repère orthonormé.
fff en bleu
f−1f^{-1}f−1en vert
Les deux courbes sont symétriques par rapport à la droite en rouge d'équation y=xy=xy=x.