Dm de maths sur les probabilités

[Pad]

Bonjour je suis en première générale et j'ai un dm de spécialité maths à rendre dans le courant de la semaine prochaine et j'ai beau essayer de comprendre comment m'y prendre je n'y arrive pas
Voici mon exercice :

Un test à été mis au point pour le dépistage d'une maladie. Le laboratoire fabricant le test, fournit les caractéristiques suivantes :
-la probabilité qu'un individu atteint par la maladie présente un test positif est 0,99
-la probabilité qu'un individu non atteint par la maladie présente un test négatif est également de 0,99.
On s'intéresse à une population cible pour laquelle on procède à un test de dépistage systématique. Un individu est choisi au hasard dans la population cible.
M désigne l'événement "l'individu choisi est malade" et T l'événement "le test de l'individu choisi est positif". On pose également p(M) =p

Voici les questions :
1- interpréter les données de l'énoncé en terme mathématiques
Ma réponse : la probabilité que l'individu choisi soit malade et présente un test positif est p de M sachant T = 0,99
La probabilité que l'individu choisi soit malade et présente un test négatif est p de M barre sachant T barre = 0,99

Mais après tout se complique.. Pourtant je suis allée voir des forum de personnes qui avaient à peut près le même énoncé mais je ne comprend toujours pas comment faire

2- exprimer la probabilité conditionnelle p de M sachant T en fonction de p
3- étudier comment varie cette probabilité conditionnelle en fonction d e la valeur de p
4- on choisit p=0,7. Expliquer ce que cela signifie pour la population cible et comparer p de M sachant T et p de M barre sachant T
5- On choisit p=0,005. La maladie étudiée est donc considérée comme "rare" dans la population cible cette fois-ci.
Comparer la probabilité pour qu'un individu qui a un test positif d'être malade puis la probabilité pour un individu qui a un test positif de ne pas être malade. Commenter ces résultats.

Cela me paraît en soit si simple mais pourtant c'est comme si mon cerveau refusait de coopérer.. Je vous en serait vraiment reconnaissante si vous m'aidiez à comprendre.
Merci d'avoir prit le temps de lire tout ça
Bonne journée

[Noemi]

@Pad Bonjour,

As tu fait un arbre ?
Le premier 0,99 correspond à la probabilité que le test soit positif sachant que l'individu est malade.

[Pad]

@Noemi
Oui j'ai fais un arbre mais pour tout ce qui est calcul je m'y perd même avec ma leçon à côté
Et merci je me confondait toujours sur les sens de M et T

[Noemi]

@Pad

Applique la relation : $P_T(M)=\frac{P(M\cap T)}{P(T)}$

[mtschoon]

Bonjour,

@Pad , je te joins un arbre pour vérification.

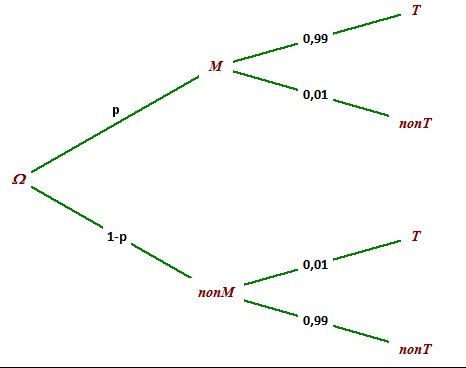
Sur cet arbre ,
$\overline{M}$ est noté nonM
$\overline{T}$ est noté nonT

Il faut que tu revois ton cours pour bien maîtriser l'utilisation de l'arbre.
Je pense que c'est là ta difficulté.

Pour la question 1), tes interprétations sont à revoir car, à cause du "et", il s'agit d'intersections.

La probabilité que l'individu choisi soit malade et présente un test positif est $p\times 0.99=0.99p$

La probabilité que l'individu choisi soit malade et présente un test négatif est $p\times 0.01=0.01p$

Pour la question 2), tu as déjà eu une aide.

$P_T(M)=\frac{P(M\cap T)}{P(T)}$

Utilise l'arbre.

$P(M\cap T)=0.09p$
$P(T)=(p\times 0.99)+(-p)\times 0.01=0.98p+0.01$

Donc : $\boxed{P_T(M)=\frac{0.99p}{0.98p+0.01}}$

Pour la question 3), étudie les variations de la fonction f définie par :
$f(p)=\frac{0.99p}{0.98p+0.01}$, p variant de 0 à 1

Pour $p=0$, $f(p)=0$.
Cette fonction est croissante.
Pour $p=1$, $f(p)=1$

Regarde cela de près .
Lorsque tu as compris, essaie de poursuivre : les questions suivantes sont des questions de calcul numérique.

Reposte si besoin.