Exercice fonction d'un repère orthonormé

Bonsoir, excusez-moi j'aurais besoin d'aide pour un exercice sur les fonctions s'il vous plaît je suis un peu en difficulté, il s'agit du début du chapitre...
J'ai simplement réussi la question 2) où je trouve (x-5)^2 pour la dérivée f(x)
Voici les questions:

calculer les limites
réaliser un tableau de variation
montrer que F(x) = -2/x-5 est une primitive de f(x)
calculer l'aire du plan compris entre la courbe , l axe des abscisses et les droites d'équations x=2 et x=4

Merci pour votre aide d'avance.

@AUDMA Bonsoir,

Quelle est l'écriture de la fonction $f$ ?

@Noemi que je suis maladroit^^ , voici la fonction f 2/(x-5)^2 definie sur ] - ∞ ; 5 [ U ] 5 ; + ∞ [

@AUDMA

C'est $\dfrac{2}{(x-5)^2}$ ?
Pour les limites, utilise les limites de référence.

$lim⁡x→−∞1x=...\displaystyle \lim_{x\to-\infty} \dfrac{1}{x}= ...$

@Noemi oui c'est bien celà, je pense que dans notre cas il faut calculer les limites en + ∞ ?mais comment faire je ne saurais pas, je dois avouer que la fonction me dérange un peu...

@AUDMA

Tu dois calculer les limites en : $−∞-\infty$ , $5^-$ , $5^+$ et $+∞+\infty$

si $x$ tend vers $−∞-\infty$ , $X = x - 5$ tend vers $−∞-\infty$ et $X^2 = (x-5)^2$ tend vers $+∞+\infty$ :
$lim⁡x→+∞1x=0+\displaystyle \lim_{x\to+\infty} \dfrac{1}{x}= 0^+$ , alors
$lim⁡x→−∞f(x)=0+\displaystyle \lim_{x\to-\infty}f(x)= 0^+$

@Noemi je pense à lim --> +∞ 2/(x-5)^2 = 0 ?

@AUDMA

Oui,

Calcul les autres limites.

@Noemi les autres ? Pour l'instant j'ai simplement remplacé x par une valeur positive et le résultat ( la courbe ) tend vers 0 mais je ne suis pas sûr de comprendre la façon de faire

@Noemi je comprends mieux malheureusement dans mon cahier il y avait pas d'exemple avec une fonction sous forme fractionnaire. Je vous remercie pour l'explication. Pour le tableau de variation il faut calculer : -4/(x-5)^3 = 0 mais encore une fois la fraction me pose problème...

@AUDMA

Pour le tableau de variations, étudie le signe de la dérivée
si $x<5x\lt 5$ et $\gt 5$

@Noemi si je comprends bien (x-5)^3 =0 est 5
Donc le tableau : https://www.cjoint.com/doc/21_11/KKBtJnHYj3o_20211127-203358.jpg

@AUDMA

Non,

Pour $x = 5$ la fonction n'est pas définie.

@Noemi il faut choisir -5 alors ? Dans ce cas-là x=-5 ca donne -1/500

@AUDMA

Pour le tableau de variation $x = 5$ est impossible donc deux traits verticaux.
Le signe à gauche est + est le signe à droite -.

@Noemi je vous remercie infiniment j'essaie de m' en sortir hélas j'ai peur que même vous vous ne pouvez rien pour moi

@AUDMA

Dans le tableau de variations que tu as transmis :
La première ligne est juste : $−∞-\infty$ ; 5 et $+∞+\infty$
La deuxième ligne : le signe de f'(x) c'est + // -
La dernière ligne les variations de $f$ ..... // ..... je te laisse compléter.

Pour la question 3. Calcule la dérivée de $F (x)$ .

Bonjour,

@AUDMA , pour que tu puisses vérifier, je te mets un schéma du tableau de variation que tu as dû trouver.
Il n'est pas parfait car les valeurs des limites sont en ligne...elles seraient mieux placées au bout des flèches...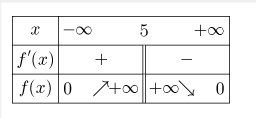

Pour la question 3, comme déjà indiqué $F^{'} (x) = f (x)$ donc F est une primitive de f.

Cela te permet de faire le calcul de la question 4)

$∫242(x−5)2dx=[−2x−5]24\displaystyle \int_2^4\dfrac{2}{(x-5)^2}dx=\biggr[\dfrac{-2}{x-5}\biggr]_2^4$ à calculer (sauf erreur, tu dois trouver $43\dfrac{4}{3}$ d'unité d'aire).

Reposte si besoin.

@Noemi merci pour l'explication du tableau de variation j'ai réussi tard le soir à le réalisé.
@mtschoon merci également à vous pour le détail du tableau de variation. Je suis arrivé a la dérivée où j'ai indiqué :
La dérivée de 1/x est -1/x^2
Et la dérivée de 1/u ( où u=x-5) est -u/u^2, avec u= x-5 on a u'=1 cela donne -1/(x-5)^2

@mtschoon j'ai trouvé je pense F'(x) = -2×1/(x-5)^2 = 2/(x-5)^2 je me lance dans l intégral !

@AUDMA

Tu as oublié un - dans le calcul de la dérivée mais le résultat final est juste.

@Noemi désolé faute de frappe ! J'ai également réussi l'intégrale ( enfin je l'espère ) : https://www.cjoint.com/doc/21_11/KKCnmb7X4V1_20211128-140800.jpg. résultat en U.a unité d'aire

@AUDMA , comme déjà indiqué, il ya un problème de signe "-" dans le calcul de F'(x) car :
$(1x−5)′=−1(x−5)2(\dfrac{1}{x-5})'=-\dfrac{1}{(x-5)^2}$
Ainsi :
$F′(x)=(−2)(−1(x−5)2)=2(x−5)2F'(x)=(-2)\biggr(-\dfrac{1}{(x-5)^2}\biggr)=\dfrac{2}{(x-5)^2}$

Ton calcul intégral est exact.

@mtschoon ça marche, je me suis trompé en tapant sur mon clavier mais j'ai bon sur mon cahier. Je vous remercie infiniment vous également Noémie pour votre aide et le temps accordez ! À une prochaine

De rien @AUDMA !
Nous faisons au mieux...
A+