Tangente communes dérivation
-
Jjulielatortue dernière édition par julielatortue
Bonjour, pourriez-vous m’aider et me guider sur cet exercice
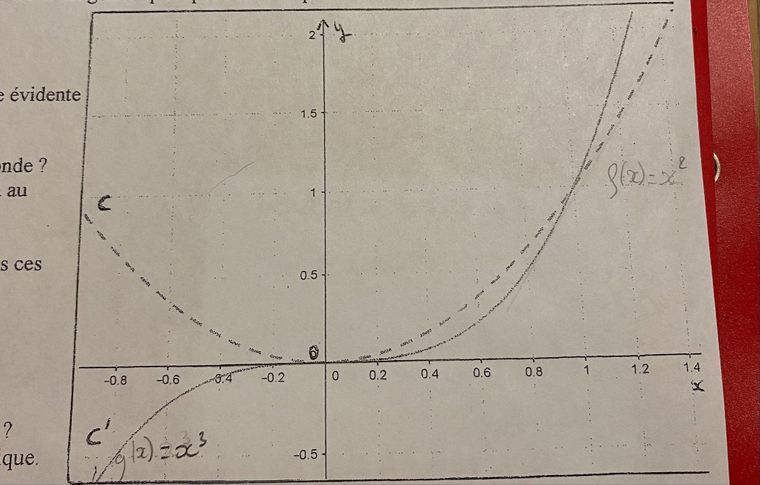
C’est le graphique d’une courbe C qui a une fonction carrée f(x)= x^^2
Et une courbe C’ qui a une fonction cube g(x)= x^^3
On a alors:
L’équation de la tangente à C en a
L’équation de la tangente à C’ en b-
Quelle tangente commune évidente peut-on donner?
-
Peut-il y en avoir une seconde? Sur quel intervalle?
Tracer la au mieux sur le graphique -
Justifier par le calcul toutes ces conjectures
-
-
Jjulielatortue dernière édition par
Ce message a été supprimé !
-
BBlack-Jack dernière édition par
Détermine les équations de la tangente à C au point d'abscisse a et de la tangente à C' au point d'abscisse b.
Tu devrais trouver :
Ta : y = 2a.x - a²
Tb : y = 3b².x - 2b³Ces tangentes sont identiques si
1°) a = b = 0 (équation des tangentes : y = 0)2°) si le système :
2a = 3b²
a² = 2b³a des solutions ...
Donc cherche si on peut trouver une valeur de a et une valeur de b (différentes de 0) telles que ce soit le cas.
...
-
Jjulielatortue dernière édition par
@Black-Jack
D'accord merci, j'ai pu mettre la photo, mais pour la question 1 et 2 je ne vois pas deux tangentes et je ne comprends pas "sur quel intervalle"
-
Jjulielatortue dernière édition par
je trouve comme équation de la tangente pour la fonction cube:
Tb= 3b^^2x-3b^^3+b^^2
Je crois que ce n'est pas normal mais je ne vois pas comment simplifier
-
@julielatortue Bonjour,
La résolution du système indiqué par Black-Jack permet de déterminer les valeurs de aaa et bbb.
Vérifie et/ou indique tes calculs.
-
Jjulielatortue dernière édition par
Est ce que l’équation de la tangente pour la fonction cube est bien égale à : 3b^^2x-2b^^3 ?
-
Jjulielatortue dernière édition par
@Noemi
Bonjour, d’accord merci
-
mtschoon dernière édition par mtschoon

Bonsoir,
@julielatortue , je peine à comprendre où tu en es exactement...
IL semble que tu aies commencé la question 3 sans avoir répondre aux deux premières.
A la question, 1," Quelle tangente commune évidente peut-on donner?" , regade le graphique ;
Au point O, l'axe des abscisses est tangente à la fois à C et à C'.
Donc , la tangente commune évidente graphiquement est l'axe des abscisses d'équation y=0.A la question 2, pour savoir sur quel intervalle il peut y voir une tangente commune à C et à C' : regarde encore le graphique.
Pour x<0, la fonction f est croissante (donc dérivée positive) alors que la fonction g est décroissante ( donc dérivée négative) .
Il ne peut donc pas y avoir de points où il y a aurait de tangente commune vu que les dérivées sont de signe contraire.
Par contre, pour x>0, les deux fonctions sont croissantes (dérivées positives donc de même signe ; c'est donc sur l'intervalle ]0,+∞[]0,+\infty[]0,+∞[, qu'il est possible de trouver une tangente commune à C et à C'.
-
mtschoon dernière édition par mtschoon

Pour la 3), tu as déjà eu de l'aide pour les équations des tangentes , mais tes propositions de calculs me semblent bizarres.
Regarde ton cours.
Tangente à C au point d'abscisse a : y=f'(a)(x-a)+f(a)
f(a)=a2f(a)=a^2f(a)=a2
f′(a)=2af'(a)=2af′(a)=2a
donc y=2a(x−a)+a2y=2a(x-a)+a^2y=2a(x−a)+a2
En développant : y=2ax−2a2+a2y=2ax-2a^2+a^2y=2ax−2a2+a2, c'est à dire :
y=2ax−a2y=2ax-a^2y=2ax−a2Même principe pour la tangente à C' au point d'anscisse b :
y=g'(b)(x-b)+f(b)
Fais le calcul et tu trouveras ce qui t'a déjà été indiqué :
y=3b2x−2b3y=3b^2x-2b^3y=3b2x−2b3Lorsque tu auras bien fait cela, il te faudra trouver a et b pour lesquels les deux tangentes sont confondues , c'est à dire ont la même équation réduite, c'est à dire
y=2ax−a2y= 2ax-a^2y=2ax−a2 indentique à y=3b2x−2b3y=3b^2x-2b^3y=3b2x−2b3, c'est à dire, comme déjà indiqué :
{2a=3b2a2=2b3\begin{cases}2a=3b^2 \cr a^2=2b^3\end{cases}{2a=3b2a2=2b3
(pense à raisonner par substitution)Bons calculs.
-
Jjulielatortue dernière édition par
@mtschoon
Oh oui d’accord je comprends mieux merci
-
Jjulielatortue dernière édition par
@mtschoon
Pour la question 3, une fois finis je pourrais vous envoyer mes calculs ?
Merci pour les réponses aux questions 1 et 2 !!
-
Jjulielatortue dernière édition par
@mtschoon Suis-je sur la bonne piste ?

-
mtschoon dernière édition par mtschoon

@julielatortue , je pense que tu n'as pas bien compris l'identification à faire. IL ne dois pas y avoir de x dans le système à résoudre.
La tangente commune, lorsqu'elle existe, s'écrit y=2ax−a2y=2ax-a^2y=2ax−a2 et y=3b2x−2b3y=3b^2x-2b^3y=3b2x−2b3
C'est à dire : pour tout xxx, 2ax−a2=3b2x−2b32ax-a^2=3b^2x-2b^32ax−a2=3b2x−2b3Par identification:
les coefficients de x sont égaux : 2a=3b22a=3b^22a=3b2
les termes constants sont égaux c'est à dire −a2=−2b3-a^2=-2b^3−a2=−2b3, c'est à dire a2=2b3a^2=2b^3a2=2b3Tu dois donc, comme déjà dit, trouver a et b vérifiant :
{2a=3b2a2=2b3\begin{cases}2a=3b^2 \cr a^2=2b^3 \end{cases}{2a=3b2a2=2b3La première équation permet d'écrire : a=32b2a=\dfrac{3}{2}b^2a=23b2
En remplaçant dans la seconde :
(32b2)2=2b3(\dfrac{3}{2}b^2)^2=2b^3(23b2)2=2b3 c'est à dire 94b4=2b3\dfrac{9}{4}b^4=2b^349b4=2b3En transposant dans le membre de gauche : 94b4−2b3=0\dfrac{9}{4}b^4-2b^3=049b4−2b3=0
Tu factorises en mettant b3b^3b3 en facteur et tu continues.
Tu dois trouver ainsi deux valeurs de bbb qui conviennent et tu en déduis les valeurs de aaa associées
Reposte si besoin.
-
mtschoon dernière édition par mtschoon

@julielatortue , pour que tu puisses vérifier tes calculs, je t'indique les résultats à trouver.
Ce ne sont que les résultats, il faut que tu fasses TOUS LES CALCULS.
b3(94b−2)=0b^3(\dfrac{9}{4}b-2)=0b3(49b−2)=0 <=>b=0b=0b=0 ou b=89b=\dfrac{8}{9}b=98
1er cas : Pour b=0\boxed{b=0}b=0, a=0\boxed{a=0}a=0
La tangente commune correspondante est la droite d'équation y=0\boxed{y=0 }y=0(axe des abscisses)Le point de contact de cette tangente aux deux courbes est le point O(0,0).
C'est ce qui avait été vu sur le graphique (question 1)2ème cas : Pour b=89\boxed{b=\dfrac{8}{9}}b=98, a=3227\boxed{a=\dfrac{32}{27}}a=2732
La tangente commune correspondante (T) a pour équation
y=6427x−1024729\boxed{y=\dfrac{64}{27}x-\dfrac{1024}{729}}y=2764x−7291024Le point de contact de cette tangente (T) à la courbe (C) est A(3227,(3227)2)A(\dfrac{32}{27},(\dfrac{32}{27})^2)A(2732,(2732)2)
Le point de contact de cette tangente (T) à la courbe (C') est B(89,(89)3)B(\dfrac{8}{9},(\dfrac{8}{9})^3)B(98,(98)3)
Remarque : les points A et B ont des abscisses strictement positives (c'est ce qui avait été indiqué, par lecture graphique, à la question 2)
Bons calculs.
-
mtschoon dernière édition par mtschoon

Illustration graphique.
Axe des abscisses (en rouge) Tangente commune. équation y=0y=0y=0
Point de contact O avec les deux courbes.Tangente commune (T) (en rouge) d'équation y=6427x−1024729y=\dfrac{64}{27}x-\dfrac{1024}{729}y=2764x−7291024
Point de contact de (T) avec (C) ( en vert) : A
Point de contact de (T) avec (C') ( en bleu) : B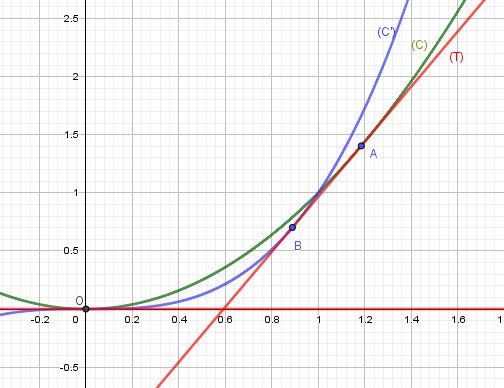
-
Jjulielatortue dernière édition par
@mtschoon
Merci beaucoup de m’avoir guidée je viens de refaire mes calculs à tête reposée et je trouve exactement comme vous. Merci pour vos explications toujours complètes et claires.
-
mtschoon dernière édition par mtschoon

@julielatortue , c'est parfait si tu as tout trouvé.
Tu as bien fait de prendre ton temps.
Lorsqu'on veut aller trop vite, on manque parfois de réflexion et on peut faire des erreurs.Tu as bien travaillé !
Bonne fin de dimanche.