Devoir sur les fonctions 1ere.

Bonjour,

J'ai un calcul que je n'arrive pas à résoudre. Est ce que quelqu'un pourrait m'aider.

La fonction f représentée par la courbe ci-dessous est de la forme f(x) = ax3 + bx2 + cx. Cette courbe passe par A (-2; 4) et B (1; 2).Déterminer graphiquement le coefficient directeur de cette tangente, puis trouver f. On donnera directement l'expression de f (x) où a, b et c sont remplacés par leur valeur.

Bonne soiree

@hugo-mt_22 Bonsoir,

Il manque la représentation graphique.

@Noemi Bonsoir je vous le donne avec la nouvelle question.

La fonction f représentée par la courbe ci-dessous est de la forme f(x)=ax3+bx2+c. Cette courbe passe par A(-1; 4) et B (5; 4) et sa tangente en A est tracée en bleu. A Déterminer graphiquement le coefficient directeur de cette tangente, puis trouver f. On donnera directement l'expression de f(x) où a, b et c sont remplaces par leur valeur.

Mais je ne sais pas comment mettre une photo.

@hugo-mt_22 Pouvez-vous m'aider?

@hugo-mt_22 , bonsoir,

C'est bizarre car les données de l'énoncé que tu donnes maintenant sont différentes du précédent...pas le même type de fonction et pas les mêmes coordonnées des points ... ?

Avec ce que tu donnes, on ne peut pas te donner de l'aide.
Il y a 3 inconnues a,b, c.
Il faut 3 équations

Avec tes données actuelles ( vérifie si ce sont les bonnes...)

$f (- 1) = 4$ <=> $a(-1)^3+b(-1)^2+c=4$
$f (5) = 4$ <=> $a(5)^3+b(5)^2+c=4$
Avec la tangente en A dont tu parles, connaissant le coefficient directeur, il y aurait la troisième équation qui serait $f^{'} (- 1) = . . . .$

Pour mettre une image situé sur ton disque dur, tu cliques sur l'icône juste au dessus du cadre texte, à droite : "Envoyer une image"

@hugo-mt_22 ,

Si tu n'arrives pas à joindre l'image, je te mets un lien qui t'explique comment déterminer graphiquement le coefficient directeur d'une droite.
https://www.youtube.com/watch?v=hpNhxEo2DsI

Si tu nous donnes le coefficient directeur de la tangente, tu pourras avoir de l'aide pour obtenir l'expression de f(x).

@mtschoon bonjour le coefficient directeur de la droite est de 4.
Merci

@hugo-mt_22 ,
C'est bien d'avoir trouvé seul le coefficient directeur de la tangente.

Je te donne des pistes avec les points A(-1,4) , B(5,4) et la courbe d'équation $f(x)=ax^3+bx^2+c$

le coefficient directeur de la tangente en A est 4.
le coefficient directeur de la tangente en A est le nombre dérivé $f^{'} (- 1)$
Tu as donc 3 conditions :
f(-1)=4
f(5)=4
f'(-1)=4

Consulte ma réponse précédente :

$f (- 1) = 4$ <=> $- a + b + b = 4$ $
$f (5) = 4$ <=> $125 a + 25 b + c = 4$

$f'(x)=3ax^2+2bx$
donc
$f^{'} (- 1) = 4$ <=> $3a(-1)^2+2b(-1)=4$ , c'est à dire
$3 a - 2 b = 4$

Pour trouver $a, b, c$ tu dois donc résoudre le système :
${−a+b+c=4125a+25b+c=43a−2b=4\begin{cases}-a+b+c=4 \cr 125a+25b+c=4 \cr 3a-2b=4\end{cases}$

Je t'indique quelques pistes mais tu dois faire tous les calculs intermédiaires.

Je te conseille d'utiliser d'abord les deux équations les plus simples :
${−a+b=4−c3a−2b=4\begin{cases}-a+b=4-c \cr 3a-2b=4\end{cases}$

Par combinaison ou substitutuion suivant tes habitudes, tu peux trouver $a$ et $b$ en fonction de $c$

Après calculs, tu dois trouver :
$a = 12 - 2 c$
$b = 16 - 3 c$

Tu remplaces $a$ et $b$ par ces expressions dans la troisième équation
$125 a + 25 b + c = 4$ ce qui te permettra, sauf erreur, de trouver $c=15827c=\dfrac{158}{27}$

Connaissant $c$ , tu en déduiras $a$ et $b$ : $a=827a=\dfrac{8}{27}$ et $b=149b=\dfrac{14}{9}$

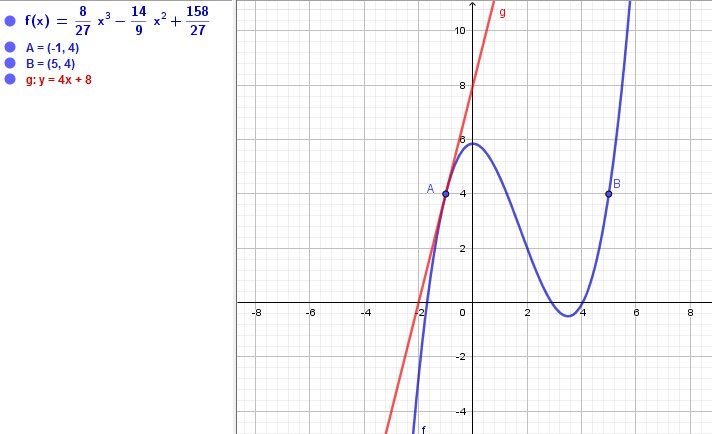
D'où $f(x)=827x3−149x2+15827f(x)=\dfrac{8}{27}x^3-\dfrac{14}{9}x^2+\dfrac{158}{27}$

Complément : je t'indique l'équation de la tangente en A :
$y = f^{'} (- 1) (x - (- 1)) + f (- 1)$ <=> $y = 4 x + 8$

Bons calculs.

Illustration graphique

989aced2-08d4-4b6a-88a4-f000e4ec950a-courbeTangente.jpg

@mtschoon merci beaucoup

@hugo-mt_22 , de rien.

C'est très bien si tu es arrivé à faire tous les calculs.

@mtschoon Bonsoir,

Soit f une fonction représentée par la courbe C ci-dessous.
Déterminer graphiquement l'équation de la tangente à C au point d'abscisse -7.
Le coefficient Directeur de la droite est de -4.

Merci

@hugo-mt_22 Bonsoir,

Si c'est un nouveau exercice, ouvre un autre sujet.
Il manque la représentation graphique.

@Noemi ok