Dérivabilité et étude de fonction
-
JJbuilder dernière édition par
Salut à vous !
S’il vous plaît j’ai un blocage avec cette question :
Soit f la fonction définie sur RRR par : f(x)=√∣x(x−2)∣−xf(x)=√|x(x-2)| -xf(x)=√∣x(x−2)∣−x
1/Justifie que f admet en 0 et en 2 des demi-tangentes dirigées toutes vers le haut.
2/Justifie que la droite d’equation y=−1y=-1y=−1 est asymptote à la courbe de f en +∞+∞+∞.Je vous remercie d’avance pour votre aide
-
@Jbuilder Bonjour,
Calcule le nombre dérivée à gauche et à droite de 0 et 2.
-
mtschoon dernière édition par mtschoon

Bonsoir;
@Noemi a dit dans Dérivabilité et étude de fonction :
@Jbuilder Bonjour,
Calcule le nombre dérivée à gauche et à droite de 0 et 2.
@Jbuilder, en fait, il n'y a pas de "nombre dérivé à gauche et à droite ni en 0 ni en 2, car si tu fais les calculs, tu dois trouver +∞+\infty+∞ et −∞-\infty−∞
Donc, fonction non dérivable ni en 0 ni en 2 , ni à droite, ni à gauche, mais deux "demi tangentes "verticales" (parallèles à l'axe des ordonnées )Je te mets des pistes de calcul pour l'étude à droite en 2
f(2)=−2f(2)=-2f(2)=−2
Pour x>2x\gt 2x>2 , x(x−2)>0x(x-2) \gt 0x(x−2)>0 donc ∣x(x−2)∣=x(x−2)|x(x-2)|=x(x-2)∣x(x−2)∣=x(x−2)
f(x)=x(x−2)−xf(x)=\sqrt{x(x-2)}-xf(x)=x(x−2)−x
Tu calcules :
limx→2,x>2f(x)−f(2)x−2=limx→2,x>2x(x−2)−x+2x−2\displaystyle \lim_{x\to 2, x\gt 2}\dfrac{f(x)-f(2)}{x-2}= \lim_{x\to 2, x\gt 2}\dfrac{\sqrt{x(x-2)}-x+2}{x-2}x→2,x>2limx−2f(x)−f(2)=x→2,x>2limx−2x(x−2)−x+2
limx→2,x>2f(x)−f(2)x−2=limx→2,x>2x(x−2)x−2−1\displaystyle \lim_{x\to 2, x\gt 2}\dfrac{f(x)-f(2)}{x-2}= \lim_{x\to 2, x\gt 2}\dfrac{\sqrt{x(x-2)}}{x-2}-1x→2,x>2limx−2f(x)−f(2)=x→2,x>2limx−2x(x−2)−1
limx→2,x>2f(x)−f(2)x−2=limx→2,x>2xx−2−1=+∞\displaystyle \lim_{x\to 2, x\gt 2}\dfrac{f(x)-f(2)}{x-2}= \lim_{x\to 2, x\gt 2}\sqrt{\dfrac{x}{x-2}}-1=+\inftyx→2,x>2limx−2f(x)−f(2)=x→2,x>2limx−2x−1=+∞
Même principe pour l'étude à gauche en 2 , mais cette fois, en prenant 0≤x<20\le x\lt 20≤x<2 , il faut prendre
f(x)=x(2−x)−xf(x)=\sqrt{x(2-x)}-xf(x)=x(2−x)−xTu trouveras limx→2,x<2f(x)−f(2)x−2=−∞\displaystyle \lim_{x\to 2, x\lt 2}\dfrac{f(x)-f(2)}{x-2}=-\inftyx→2,x<2limx−2f(x)−f(2)=−∞
Le principe en 0 est le même.
Bons calculs.
-
mtschoon dernière édition par mtschoon

Illustration graphique.
Courbe en rouge.
Demi-tangentes "verticales" en bleu.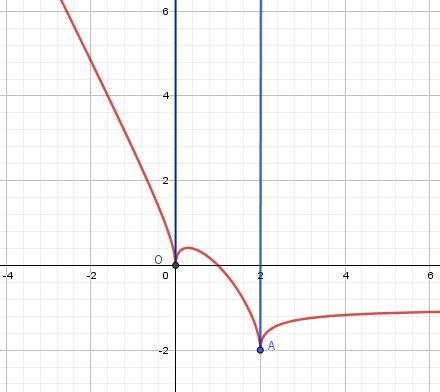
-
mtschoon dernière édition par mtschoon

@Jbuilder , lorsque tu auras bien étudié ta première question , tu pourras passer à la seconde.
Pour faire la justification demandée, il suffira que tu prouver que :
limx→+∞f(x)−(−1)=0\displaystyle \lim_{x\to +\infty} f(x)-(-1)=0x→+∞limf(x)−(−1)=0Vu que dans ce cax, x(x−2)>0x(x-2) \gt 0x(x−2)>0, il suffira de prouver que :
limx→+∞x(x−2)−(−1)=0\displaystyle \lim_{x\to +\infty} \sqrt{x(x-2)}-(-1)=0x→+∞limx(x−2)−(−1)=0Bons calculs.
Reposte si besoin.
-
JJbuilder dernière édition par
@mtschoon
Merci infiniment à vous j’ai bien compris la démarche
infiniment à vous j’ai bien compris la démarche
-
mtschoon dernière édition par

De rien @Jbuilder , c'est parfait si tu as compris.
J'espère que tu es arrivé à lever l'indétermination pour trouver la limite de la question 2 (sinon, demande).