(limite à gauche et limite à droite )
-
Wwalter dernière édition par
Bonjour
Est ce que quelqu'un peut m'expliquer, quand devrait-on chercher les limites à gauche et à droite!?
-
mtschoon dernière édition par mtschoon

@walter , bonjour,
Je ne vais pas te donner une liste des cas pour lesquels il faut chercher la limite à gauche et la limite à droite ! ce serait improductif.S'il s'agit d'une limite en x0x_0x0, il faut analyser le comportement de la fonction au voisinage de x0x_0x0,
Si cela le nécessite, tu fais deux cas (à gauche et à droite) , sinon tu n'en fait qu'un.Je te donne quelques exemples pour t'éclairer.
1 ) Soit f(x)=e1x\boxed{f(x)=e^{\dfrac{1}{x}}}f(x)=ex1
Cette fonction est définie sur R∗R^*R∗
On recherche la limite possible en 0.
Lorsque x tend vers 0 par valeurs positives, 1x\dfrac{1}{x}x1 tend vers +∞+\infty+∞
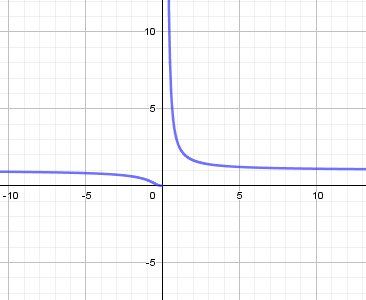
Donc e1xe^{\dfrac{1}{x}}ex1 tend vers +∞\infty∞limx→0+f(x)=+∞\displaystyle \lim_{x\to 0^+}f(x)=+\inftyx→0+limf(x)=+∞ (limite à droite infinie)
Lorsque x tend vers 0 par valeurs négatives, 1x\dfrac{1}{x}x1 tend vers −∞-\infty−∞
Donc e1xe^{\dfrac{1}{x}}ex1 tend vers 000limx→0−f(x)=0\displaystyle \lim_{x\to 0^-}f(x)=0x→0−limf(x)=0 (limite à gauche finie)
Illustration graphique :
-
mtschoon dernière édition par mtschoon

2 ) Soit g(x)=e1x2\boxed{g(x)=e^{\dfrac{1}{x^2}}}g(x)=ex21
Cette fonction est définie sur R∗R^*R∗On recherche la limite possible en 0.
Lorsque x tend vers 0, que ce soit par valeurs positives ou négatives, x2x^2x2 tend vers 0 par valeurs positives ( vu qu'il s'agit d'un carré), donc 1x2\dfrac{1}{x^2}x21 tend vers +∞\infty∞
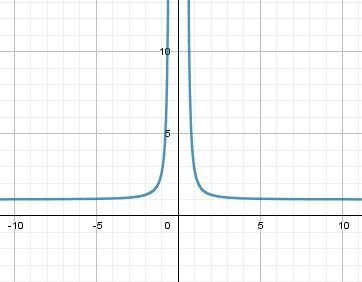
Donc e1x2e^{\dfrac{1}{x^2}}ex21 tend vers +∞\infty∞limx→0g(x)=+∞\displaystyle \lim_{x\to 0}g(x)=+\inftyx→0limg(x)=+∞
Ce n'était pas utile de distinguer les cas x>0x\gt0x>0 et x<0x\lt 0x<0 vu que le comportement de la fonction g était le même dans les deux cas.
Illustration graphique :
-
mtschoon dernière édition par mtschoon

3 ) Soit h(x)=E(x)\boxed{h(x)=E(x)}h(x)=E(x)
Cette fonction EEE est la fonction "partie entière"
Elle est définie sur RRR
Par définition :
Soit n un entier quelconque de ZZZ ,
pour tout xxx de [n,n+1[n,n+1[n,n+1[, E(x)=nE(x)=nE(x)=nOn recherche la limite possible en 1.
On est obligé de distinguer les cas x>1 et x<1 vu que le comportement de la fonction h n'est pas le même dans les deux cas.
Pour x∈[1,2[,h(x)=1x\in [1,2[, h(x)=1x∈[1,2[,h(x)=1 (fonction constante sur l'intervalle [1,2[)
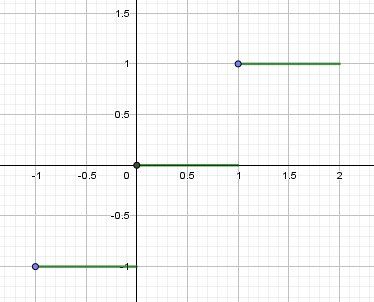
Donc limx→1,x>1h(x)=1\displaystyle \lim_{x\to 1, x\gt 1}h(x)=1x→1,x>1limh(x)=1 (limite à droite finie)
Pour x∈[0,1[,h(x)=0x\in [0,1[, h(x)=0x∈[0,1[,h(x)=0 ( fonction constante sur l'intervalle [0,1[ )
Donc limx→1,x<1h(x)=0\displaystyle \lim_{x\to 1, x\lt 1}h(x)=0x→1,x<1limh(x)=0 (limite à gauche finie)
Remarque relative à la continuité.
h(1)=E(1)=1h(1)=E(1)=1h(1)=E(1)=1
Vu que limx→1,x>1h(x)=h(1)\displaystyle \lim_{x\to 1, x\gt 1}h(x)=h(1)x→1,x>1limh(x)=h(1), la fonction est continue à droite en 1.
Vu que limx→1,x<1h(x)≠h(1)\displaystyle \lim_{x\to 1, x\lt 1}h(x)\ne h(1)x→1,x<1limh(x)=h(1), la fonction n'est pas continue à gauche en 1.Illustration graphique :
Bonne réflexion.