Etude de fonction racine cubique
-
MMohssine dernière édition par Noemi
Bonjour,
Etudier les variations de f sur Df
f(x)=x4−x3f(x)=x\sqrt[3]{4-x}f(x)=x34−x
-
@Mohssine Bonjour,
Calcule la dérivée de la fonction.
-
Lloicstephan dernière édition par
@Noemi
je pense qu'il doit s"appuyer sur la derrivéé d'un produit de deux fonctions sauf erreur
(fg)′=f′g+g′f(fg)'=f'g+g'f(fg)′=f′g+g′f
-
mtschoon dernière édition par mtschoon

Bonsoir,
@Mohssine a dit dans Etude de fonction racine cubique :
tions >Etudier les variations de f sur Df
f(x)=x4−x3f(x)=x\sqrt[3]{4-x}f(x)=x34−x@Mohssine , la première chose à faire c'est de donner Df ou de l'indiquer si l'énoncé te le donne pas.
Merci de préciser cela.Il faut savoir sur quel ensemble tu travailles, pour calculer dérivée, et étudier les variations.
-
Lloicstephan dernière édition par
effectivement etant donne que x peut etre dans R et la racine a sa restiction !
-
En prenant comme domaine de définition : Df=RD_f= \RDf=R.
La dérivée :
f′(x)=(4−x)13−x×13(4−x)−23f'(x) = (4-x)^{\frac{1}{3}}-x\times \dfrac{1}{3}(4-x)^{-\frac{2}{3}}f′(x)=(4−x)31−x×31(4−x)−32A réduire au même dénominateur et à simplifier.
Un point particulier à étudier A(4;0)A(4;0)A(4;0)
-
mtschoon dernière édition par mtschoon

Bonjour,
Je me permets une nuance et c'est pourquoi que je demandais à @Mohssine d'indiquer son domaine de définition et j'aurais voulu qu'il le donne.
Pour la "fonction racine cubique", comme indiqué, le domaine est RRR, car x3\sqrt[3]x3x est le réel dont la puissance 3 vaut x.
exemples : 83=2\sqrt[3]8=238=2 car 23=82^3=823=8 et −83=−2\sqrt[3]{-8}=-23−8=−2 car (−2)3=−8(-2)^3=-8(−2)3=−8xxx et x3\sqrt[3]x3x sont de même signe.
La dérivée de x3\sqrt[3]x3x sur R∗R^*R∗ vaut 13(x3))2\dfrac{1}{3(\sqrt[3] x))^2}3(3x))21
La "fonction puissance" x13x^\frac{1}{3}x31 vaut "racine cubique de x" seulement pour x>0\boxed{x\gt 0}x>0 vu que x13=e13ln(x)x^{\dfrac{1}{3}}=e^{\dfrac{1}{3}ln(x)}x31=e31ln(x)
Donc, vu l'énoncé, on doit travailler sur RRR, donc on doit utiliser la fonction "racine cubique" (et pas la fonction puissance qui change le domaine de définition)
Pour x≠4x\ne 4x=4 , la dérivée s'écrit donc (dérivée d'un produit , comme l'indique @loicstephan )
f′(x)=4−x3−x3(4−x3)2f'(x)=\sqrt[3] {4-x}-\dfrac{x}{3(\sqrt[3] {4-x})^2}f′(x)=34−x−3(34−x)2xf′(x)=3(4−x3)3−x3(4−x3)2f'(x)=\dfrac{3(\sqrt[3]{4-x})^3-x}{3(\sqrt[3]{4-x})^2}f′(x)=3(34−x)23(34−x)3−x
f′(x)=3(4−x)−x3(4−x3)2f'(x)=\dfrac{3(4-x)-x}{3(\sqrt[3]{4-x})^2}f′(x)=3(34−x)23(4−x)−x
(numérateur à simplifier)
@Mohssine , consulte ton cours, regarde tout ça de près, et poursuit l'étude.
Reposte si besoin, bien sûr.
-
MMohssine dernière édition par
@mtschoon Bonjour, on considère que la fonction racine est définit sur R plus, alors l'étude de la fonction est sur 4 plus l'infini.
-
mtschoon dernière édition par mtschoon

Merci pour ta réponse @Mohssine .
C'était cela que je voulais savoir depuis le début !
Si , dans ton cours, la fonction racine cubique est définie dans R+R+R+ , c'est beaucoup plus simple !
Dans ce cas, la fonction racine cubique prend la valeur 000 pour x=0x=0x=0 et tu peux utiliser la forme puissance 13\dfrac{1}{3}31 si tu préfères pour x>0x\gt 0x>0
Par contre , dans ton exercice, Df n'est pas ce que tu indiques.
4−x≥04-x\ge 04−x≥0 <=> 4≥x4\ge x4≥x <=> x≤4\boxed{x\le 4}x≤4
Tu travailles donc , dans ton exercice, sur Df=]−∞,4]Df=]-\infty, 4]Df=]−∞,4]
Remarque : d'après ce que tu indiques de ton cours, cette fonction f est est définie sur ]−∞,4]]-\infty, 4]]−∞,4] ; elle prend la valeur 000 pour x=4x=4x=4 ; elle est dérivable sur ]−∞,4[]-\infty, 4[]−∞,4[
-
MMohssine dernière édition par
@mtschoon Pardon, j'étais dans l'exercice que je viens de poster là je vais ouvrir celuilà et écrire les résultas que j'ai obtenus
-
mtschoon dernière édition par

@Mohssine, OK
-
mtschoon dernière édition par mtschoon

Pour que tu puisses vérifier tes calculs, je t'indique ce que tu dois trouver pour les variations de f :
f strictement croissante sur ]−∞,3]]-\infty, 3]]−∞,3]
f(3)=3f(3)=3f(3)=3
f strictement décroissante sur [3,4][3,4][3,4]
f(4)=0f(4)=0f(4)=0Si des compléments sont exigés (?) :
f non dérivable, à gauche, pour x=4x=4x=4 (le taux permet d'obtenir -∞\infty∞, donc demi-tangente parallèle à l'axe des ordonnées).
Lorsque xxx tend vers −∞-\infty−∞, la fonction tend vers −∞-\infty−∞
Tout ceci est à prouver.
-
MMohssine dernière édition par
@Mohssine un excercice sur la concavité
-
MMohssine dernière édition par
@mtschoon est ce que vous avez vu l'autre exo; on demande aussi la graphe de la fonction
-
mtschoon dernière édition par mtschoon

@Mohssine , si tu parles de la fonction de cette discussion ( je n'ai pas regardé ton topic sur la concavité car j'ai vu que deux intervenants s'en occupaient), je te joins un graphique, mais ce n'est qu'une illustration (graphique).
On le fait lorsque tout a été démontré.La courbe est en bleu.
La demi-tangente "verticale" au point A(4,0) est en rouge.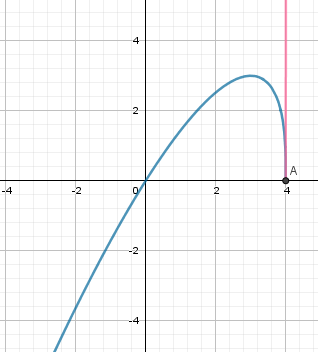
-
MMohssine dernière édition par
@mtschoon on est encore sur le meme probleme ce n'est pas encore résolu; je parle du probleme de concavité