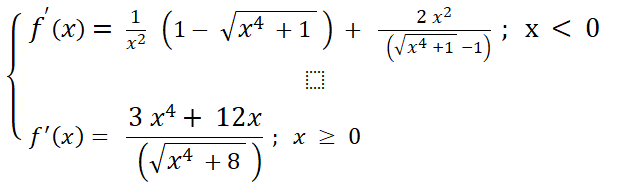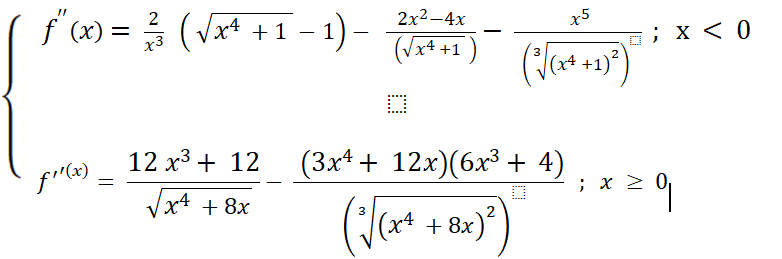Etude de concavité de fonction
-
MMohssine dernière édition par Noemi
Bonjour, etudier la concavité de f
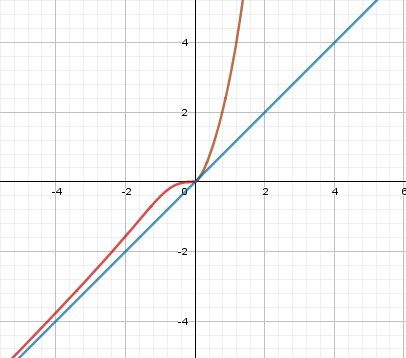
{f(x)=x4+1−1x si x<0f(x)=xx4+8x si x≥0\begin{cases} f(x)=\dfrac{\sqrt{x^4+1}-1}{x} \ si \ x\lt0 \cr \cr f(x)=x\sqrt{x^4+8x} \ si \ x\geq0 \end{cases}⎩⎪⎪⎪⎨⎪⎪⎪⎧f(x)=xx4+1−1 si x<0f(x)=xx4+8x si x≥0
Fonction écrite en Latex par la modération.
je trouve des la premiere le résultat suivant , il reste a calculer la dérivée seconde
-
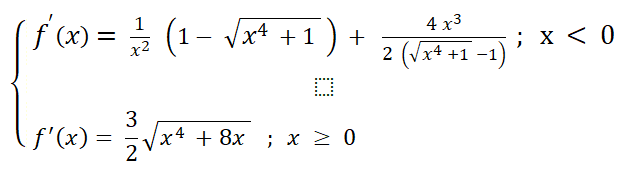
MMohssine dernière édition par
@Mohssine
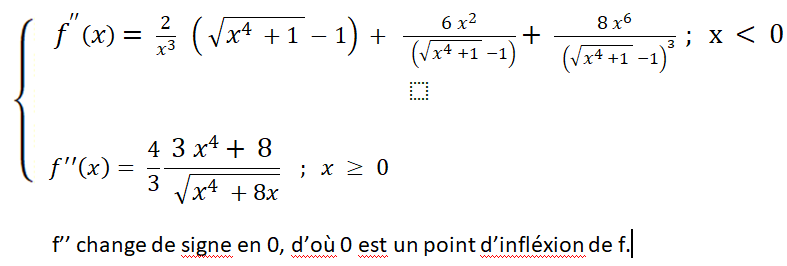je ne suis pas si sure des calculs
-
@Mohssine Bonjour,
Vérifie les calculs pour la dérivée.
-
MMohssine dernière édition par
@Noemi 2x carrée au lieu de x3 Ok
-
MMohssine dernière édition par
@Mohssine On demande de tracer la courbe aussi
-
BBlack-Jack dernière édition par
Bonjour,
Pour moi :
Pour x < 0 :
f'(x) = 2x²/V(x^4 + 1) - (V(x^4+1)-1)/x² (Avec V pour racine carrée)pour x >= 0
f'(x) = 3(x³+2)/V(x²+4x) (Avec V pour racine carrée)N'étant déjà pas d'accord sur les dérivées premières ... inutile de vérifier pour tes dérivées secondes.
Vérifie tes calculs
-
MMohssine dernière édition par
@Black-Jack je trouve ca
-
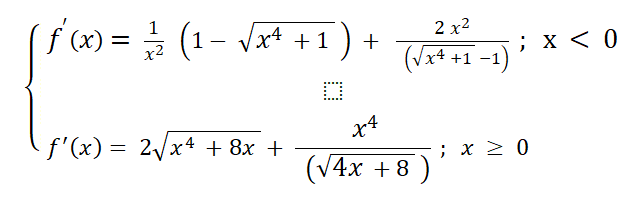
MMohssine dernière édition par
-
Pour la première réponse,
Le terme de droite de la première dérivée est faux.
Les deux termes de la seconde dérivée sont faux.Pour les deux dérivées, il faut réduire au même dénominateur.
-
MMohssine dernière édition par
@Noemi je viens de poster un autre calcul
-
Le terme de droite de la première dérivée doit être : 2x2x4+1\dfrac{2x^2}{\sqrt{x^4+1}}x4+12x2
La deuxième dérivée, il manque un xxx au dénominateur.
-
MMohssine dernière édition par
@Noemi oui enfin les calcul de f' est juste
il reste de calculer f'' pour tracer la courbe
-
Indique tes résultats.
-
MMohssine dernière édition par
-
Vérifie tes calculs.
Pour la première dérivée, tu devrais d'abord simplifier f′(x)f'(x)f′(x).
-
MMohssine dernière édition par
@Noemi comment la simplifier c'est ca la question
-
Tu réduis au même dénominateur.
f′(x)=1−x4+1x2+2x2x4+1f'(x) = \dfrac{1-\sqrt{x^4+1}}{x^2}+\dfrac{2x^2}{\sqrt{x^4+1}}f′(x)=x21−x4+1+x4+12x2
f′(x)=(1−x4+1)(x4+1)+2x2×x2x2×x4+1=...f'(x)= \dfrac{(1-\sqrt{x^4+1})(\sqrt{x^4+1})+2x^2\times x^2}{x^2\times \sqrt{x^4+1}}= ...f′(x)=x2×x4+1(1−x4+1)(x4+1)+2x2×x2=...
-
MMohssine dernière édition par
@Noemi ca donne
-
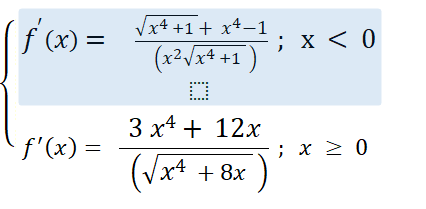
C'est juste.
-
MMohssine dernière édition par
@Mohssine mnt est ce que le f'' est correcte ?
-
As-tu rectifié les dérivées secondes ?
-
MMohssine dernière édition par
@Noemi sont t ils pas correcte comme mentionées avant?
-
J'ai indiqué de vérifier les calculs.
Pourquoi calculer les dérivées seconde ?
-
MMohssine dernière édition par
@Noemi on demande d'étudier la concavité de f
-
Donc vérifie tes calculs pour la dérivée seconde.
-
MMohssine dernière édition par
@Noemi je sais pas pk on intervient sur les problemes qu'on ne sait pas résourde pk ne pas se taire par exemple c'est bcp plus mieux
-
mtschoon dernière édition par mtschoon
@Mohssine , bonjour,
Je viens de calculer au brouillon les dérivées secondesPourx≥0x\ge 0x≥0, f′′(x)f''(x)f′′(x) est assez simple et le signe (positif) est facile à déduire.
Par contre, pour x<0x\lt 0x<0 , l'expression que je trouve est moche...
Je l'ignore bien sûr, mais je suis surprise que tu doives passer par ces calculs...Regarde bien l'énoncé qui t'est proposé.
L'étude de la concavité est-elle demandée : avant la représentation graphique ou après ?
Si la concavité était demandée après le graphique(?) , tu pourrais étudier le signe de f'(x) (tu as déjà les dérivées), faire le tableau de variations, la courbe et graphiquement déduire la concavité.
A toute fin utile, je te joins le graphique :
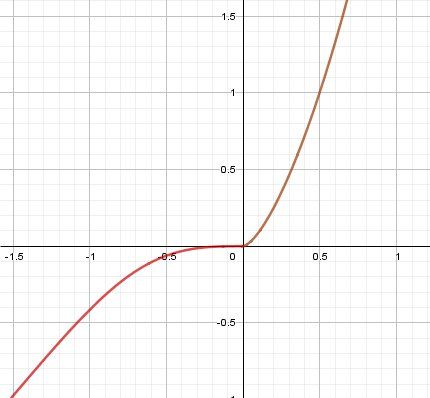
Je te mets aussi un lien pour étudier graphiquement la concavité.
-
MMohssine dernière édition par
@mtschoon Bonjour, j'ai obtenu une graphe resemblant a la votre ,
mais il semble j'ai une erreur dans l'etude des branches infinis, voici mes résultats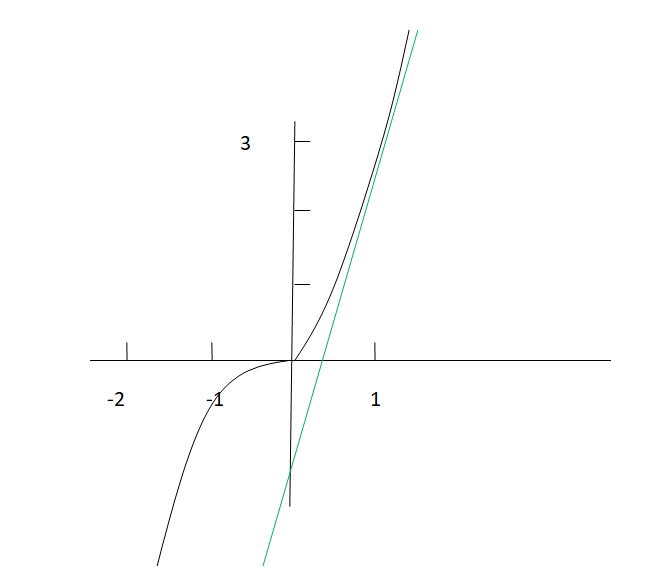
-
MMohssine dernière édition par
@mtschoon On demande d'etudier la concavité puis de dessiner Cf
-
mtschoon dernière édition par mtschoon
Je ne vois pas à quoi correspond la droite en vert dans ton schéma ...
Pour +∞+\infty+∞, f(x)x\dfrac{f(x)}{x}xf(x) tend bien vers +∞+\infty+∞
Par contre, pour −∞-\infty−∞, ce n'est pas bon.
En multipliant le numérateur et le dénominateur par le conjugué du numérateur, après transformations, tu dois trouver :
limx→−∞f(x)x=1\displaystyle \lim_{x\to -\infty}\dfrac{f(x)}{x}=1x→−∞limxf(x)=1
-
mtschoon dernière édition par mtschoon
@Mohssine, je termine l'étude à −∞-\infty−∞,
Tu as donc limx→−∞f(x)x=1\displaystyle \lim_{x\to -\infty}\dfrac{f(x)}{x}=1x→−∞limxf(x)=1
a=1a=1a=1Tu peux chercher s'il existe une asymptote oblique d'équation y=ax+by=ax+by=ax+b
Après calcul , tu dois trouver :
limx→−∞f(x)−ax=limx→−∞f(x)−x=0\displaystyle \lim_{x\to -\infty}f(x)-ax= \displaystyle \lim_{x\to -\infty}f(x)-x=0x→−∞limf(x)−ax=x→−∞limf(x)−x=0
donc b=0b=0b=0
Conclusion : asymptote oblique d'équation y=x\boxed{y=x}y=x ( en −∞-\infty−∞ )
-
mtschoon dernière édition par mtschoon
Représentation graphique (avec les unités adaptées) pour bien "voir" l'asymptote oblique en −∞-\infty−∞ (couleur bleue)
