3. La partie entière et la période ( les fonctions)

La partie entière et la période ( les fonctions)

  • A

    Bonjour ...
    J'ai besoin d'aide, et merci d'avance ....
    On considère la fonction :
    R(x)(-1)^E(x)×(x-E(x))×(E(x)-x+1)

    1. Montrer que R est périodique de période appartient à N
    2. a_ Donner une autre expression à R
      b_ Construire la courbe de la restriction de R sur [-4;4]
    N 1 réponse
  • N
    Modérateurs

    @ASMAE Bonjour,

    La fonction est -elle bien R(x)=(−1)E(x)×(x−E(x))×(E(x)−x+1)R(x)= (-1)^{E(x)}\times (x-E(x))\times (E(x)-x+1)R(x)=(−1)E(x)×(x−E(x))×(E(x)−x+1) ?

    Exprime et simplifie R(x+n)R(x+n)R(x+n).

    R(x+n)=(−1)E(x+n)×(x+n−E(x+n))×(E(x+n)−x−n+1)=...R(x+n)= (-1)^{E(x+n)}\times (x+n-E(x+n))\times (E(x+n)-x-n+1)= ...R(x+n)=(−1)E(x+n)×(x+n−E(x+n))×(E(x+n)−x−n+1)=...

    A 1 réponse
  • A

    @Noemi
    Oui la fonction est : R(x)=(−1)E(x)×(x−E(x))×(E(x)−x+1) 
    Pouvez-vous compléter la solution ??
    Merci d'avance

    N 1 réponse
  • N
    Modérateurs

    @ASMAE

    Simplifie l'expression que j'ai indiquée.

    A 1 réponse
  • mtschoon

    Bonjour,

    @ASMAE , si tu souhaites un"racourci"...

    (-1) est à la puissance E(x)
    On recherche un naturel n de N∗N^*N∗tel que
    (−1)E(x+n)=(−1)E(x)(-1)^{E(x+n)}=(-1)^{E(x)}(−1)E(x+n)=(−1)E(x)
    (−1)E(x)+n=(−1)E(x)(-1)^{E(x)+n}=(-1)^{E(x)}(−1)E(x)+n=(−1)E(x)
    (−1)E(x)(−1)n=(−1)E(x)(-1)^{E(x)}(-1)^n=(-1)^{E(x)}(−1)E(x)(−1)n=(−1)E(x)
    n doit être pair pour que (−1)n=1(-1)^n=1(−1)n=1
    Le plus petit naturel pair non nul est 2

    Essaie donc de calculer R(x+2)R(x+2)R(x+2) et tu verras que tu trouveras (après simplification) R(x)R(x)R(x)

    A 1 réponse
  • A

    @Noemi j'ai obtenue
    R(x+n)=(−1)^E(x)×(x−E(x))×(E(x)−x+1) 
    Ce la veut dire que R(x+n)=R(x)
    Mais comment je peux trouver la valeur de n ?

    N 1 réponse
  • A

    @mtschoon
    Je pense qu'on peut pas travailler avec ta méthode car on sait pas que (-1)^E(x)=(-1)^E(x+n) !!!?

  • N
    Modérateurs

    @ASMAE

    Tu as oublié un terme :
    R(x+n)=(−1)E(x+n)×(x+n−E(x+n))×(E(x+n)−x−n+1)R(x+n)= (-1)^{E(x+n)}\times (x+n-E(x+n))\times (E(x+n)-x-n+1)R(x+n)=(−1)E(x+n)×(x+n−E(x+n))×(E(x+n)−x−n+1)
    R(x+n)=(−1)E(x)×(−1)n×(x−E(x))×(E(x)−x+1)R(x+n)= (-1)^{E(x)}\times (-1)^n\times (x-E(x))\times (E(x)-x+1)R(x+n)=(−1)E(x)×(−1)n×(x−E(x))×(E(x)−x+1)
    R(x+n)=(−1)n×R(n)R(x+n)=(-1)^n\times R(n)R(x+n)=(−1)n×R(n)
    Donc tu en déduis nnn pour la période.

    A 1 réponse
  • A

    @Noemi
    Comment je dois faire la déduction?

    N 1 réponse
  • mtschoon

    Bonsoir,

    @ASMAE ,

    Si tu regardais avec soin ce que je t'ai indiqué, tu aurais la réponse à la déduction...

  • N
    Modérateurs

    @ASMAE

    R(x+n)=(−1)n×R(n)R(x+n)=(-1)^n\times R(n)R(x+n)=(−1)n×R(n)
    Quelle valeur (le plus petit entier) faut-il donner à nnn pour que :
    (−1)n×R(n)=R(n)(-1)^n\times R(n)= R(n)(−1)n×R(n)=R(n) ?

    A 1 réponse
  • A

    @Noemi
    Je pense que c'est 0

    N 1 réponse
  • N
    Modérateurs

    @ASMAE

    On cherche un entier supérieur à 0.

    A 1 réponse
  • A

    @Noemi
    Mais pourquoi supérieur à 0 ?
    Alore c'est 2

    N 1 réponse
  • N
    Modérateurs

    @ASMAE

    La définition de période:
    On dit qu'une fonction fff est périodique s'il existe un nombre réel non nul uuu vérifiant la propriété suivante :
    x∈Dfx∈Dfx∈Df, (x+u)∈Df(x + u)∈Df(x+u)∈Df et f(x+u)=f(x)f(x + u) = f(x)f(x+u)=f(x).

    On cherche donc une valeur de nnn tel que R(x+n)=R(x)R(x+n)= R(x)R(x+n)=R(x), nnn est supérieur à 0.
    Donc la période est bien 2.

    A 2 réponses
  • A

    @Noemi
    Ah ok
    J'ai bien compris merci infiniment 😁

  • mtschoon

    Bonsoir,

    Pour consultation éventuelle,

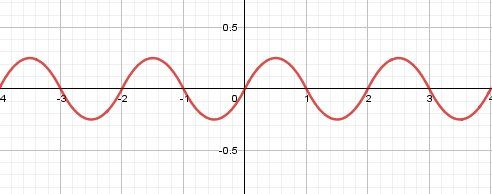
    Représentation graphique de R sur [0,2[[0,2[[0,2[, c'est à dire sur une période :
    Pour x∈[0,1[x\in [0,1[x∈[0,1[, E(x)=0E(x)=0E(x)=0 d'où R(x)=−x2+xR(x)=-x^2+xR(x)=−x2+x
    Pour x∈[1,2[x\in [1,2[x∈[1,2[, E(x)=1E(x)=1E(x)=1 d'où R(x)=x2−3x+2R(x)=x^2-3x+2R(x)=x2−3x+2

    La courbe se complète, sur RRR, par périodicité.

    46c85997-b195-4b1b-ba6e-80b891c966fa-floor.jpg

    A 1 réponse
  • A

    @mtschoon grand merci
    Pouvez-vous me donner une autre expression à R ?

  • A

    @Noemi pouvez-vous m'aider à trouver une autre expression de R?

  • mtschoon

    @ASMAE , avec les parties entières, on procède par intervalle.

    Tu peux dire, par exemple, que pour tout kkk de ZZZ :
    Pour tout xxx de [k,k+1[[k,k+1[[k,k+1[ , R(x)=(−1)k(x−k)(k−x+1)R(x)=(-1)^k(x-k)(k-x+1)R(x)=(−1)k(x−k)(k−x+1)

    En détaillant :
    Si kkk est pair, R(x)=(x−k)(k−x+1)R(x)=(x-k)(k-x+1)R(x)=(x−k)(k−x+1)
    Si kkk est impair : R(x)=−(x−k)(k−x+1)R(x)=-(x-k)(k-x+1)R(x)=−(x−k)(k−x+1)

    Remarque : en principe, comme déjà dit, on étudie la fonction sur une période (c'est le but d'avoir trouvé la période, c'est à dire ici on étudie R sur [0,2[[0,2[[0,2[, et ensuite, pour le graphique, on complète par périodicité.

    A 1 réponse
  • A

    @mtschoon j'ai pas compris 🙂🙂
    Est'ce qu'on peut étudier l'expression de R par les intervalles
    Par exemple : Si x appartient [0;1[ , et je donne l'expression de R sur cet intervalle
    Puis je fais la même chose avec x de l'intervalle [1;2[

    N 1 réponse
  • N
    Modérateurs

    @ASMAE

    Oui, indique l'écriture de la fonction sur chaque intervalles (la réponse a été donnée par mtschoon),
    Pour x∈[0,1[x\in [0,1[x∈[0,1[, E(x)=0E(x)=0E(x)=0 d'où R(x)=x(−x+1)=−x2+xR(x)=x(-x+1)=-x^2+xR(x)=x(−x+1)=−x2+x
    Pour x∈[1,2[x\in [1,2[x∈[1,2[, E(x)=1E(x)=1E(x)=1 d'où R(x)=−(x−1)(1−x+1)=x2−3x+2R(x)=-(x-1)(1-x+1)=x^2-3x+2R(x)=−(x−1)(1−x+1)=x2−3x+2

    puis tu précises que la fonction est périodique avec R(x+2)=R(x)R(x+2)=R(x)R(x+2)=R(x).

    A 1 réponse
  • A

    @Noemi
    D'accord, Merci

  • mtschoon

    @ASMAE , si maintenant tu as bien compris le cas [0,2[ décomposé en deux-sous-cas [0,1[ et [1,2[,bien sûr, avant de faire le graphique, il faut faire l'étude soignée.

    Pour x∈[0,1[,R(x)=−x2+xx\in [0,1[, R(x)=-x^2+xx∈[0,1[,R(x)=−x2+x
    R′(x)=−2x+1R'(x)=-2x+1R′(x)=−2x+1
    Etude du signe de R′(x)R'(x)R′(x) et tableau de variation sur [0,1[[0,1[[0,1[
    Graphique : Portion de parabole (P1)

    Pour x∈[1,2[,R(x)=x2−3x+2x\in [1,2[, R(x)=x^2-3x+2x∈[1,2[,R(x)=x2−3x+2
    R′(x)=2x−3R'(x)=2x-3R′(x)=2x−3
    Etude du signe de R′(x)R'(x)R′(x) et tableau de variation sur [1,2[[1,2[[1,2[
    Graphique : Portion de parabole (P2)

    Si tu le souhaites, tu peux résumer les deux tableaux de variation en un seul avec x∈[0,2[x\in [0,2[x∈[0,2[

    En complément, tu peux démontrer que (P1) et P(2) sont symétriques par rapport au point I(1,0)
    Par exemple : avec hhh compris entre 000 et 111
    Pour x=1−hx=1-hx=1−h
    R(1−h)=−(1−h)2+(1−h)=−h2+hR(1-h)=-(1-h)^2+(1-h)=-h^2+hR(1−h)=−(1−h)2+(1−h)=−h2+h
    Pour x=1+hx=1+hx=1+h
    R(1+h)=(1+h)2−3(1+h)+2=h2−hR(1+h)=(1+h)^2-3(1+h)+2=h^2-hR(1+h)=(1+h)2−3(1+h)+2=h2−h
    Les ordonnées obtenues sont opposées : R(1+h)=−R(1−h)R(1+h)=-R(1-h)R(1+h)=−R(1−h)

    Lorsque cette construction sur [0,2[[0,2[[0,2[ est bien faite, par translations de vecteur 2i→2\overrightarrow{i}2i ou −2i→-2\overrightarrow{i}−2i (en appelant i→\overrightarrow{i}i le vecteur directeur de l'axe des abscisses) , tu complètes pour avoir la courbe sur l'intervalle demandé par l'énoncé.

    Bon travail.

    A 1 réponse
  • A

    @mtschoon
    J'ai bien compris, Merci d'avoir m'aider 😁🤍

  • mtschoon

    Bon travail @ASMAE

    On fait au mieux pour aider.

Se connecter pour répondre