lim convergente et reciproque

bjrr!
on me demande maintenant d'utilier le taux de croissance pour montrer que si une suite $U_n$ converge vers $l$ alors limite $U_{n+1}=l$ et de montrer que la reciproque est fausse
merci de bien vouloir m'aider

@loicstephan Bonsoir,

Montre que la différence entre deux termes consécutifs tend vers 0.
Pour la réciproque utilise la suite $U_n=ln(n)$ .

@Noemi
il m'es demande d'utiliser le taux d'accroissement pour montre que la reciproque est fausse
en ce qui concerne la premiere le theoreme de l'unicite de la limite peut me permettre de montrer?

@loicstephan

Ce n'est pas ce que tu as écrit dans le premier message.

Il faut montrer que $U_n-U_{n+1}$ tend vers 0.
$∣Un−Un+1∣=∣Un−l+l−Un+1∣≤∣Un−l∣+∣Un+1−l∣\vert U_n-U_{n+1}\vert = \vert U_n-l+l-U_{n+1}\vert \leq \vert U_n-l\vert +\vert U_{n+1}-l\vert$

Étant donné $ϵ>0\epsilon \gt 0$ , on pose $ϵ1=ϵ2\epsilon_1 = \dfrac{\epsilon}{2}$ .
Puisque la limite de la suite $U_n$ est $l$ , il existe un entier positif $nϵ1n_{\epsilon_1}$ tel que, pour tout $\geq n_{\epsilon_1}$ on a $∣Un−l∣<ϵ1\vert U_n-l\vert \lt \epsilon_1$ .
Donc, si $\geq n_{\epsilon_1} + 1$
$∣Un−Un+1∣≤∣Un−l∣+∣Un+1−l∣≤ϵ1+ϵ1=ϵ\vert U_n-U_{n+1}\vert \leq \vert U_n-l\vert +\vert U_{n+1}-l\vert \leq \epsilon_1+\epsilon_1=\epsilon$
D'ou $U_n-U_{n+1}$ tend vers 0.
Tu peux conclure.

@Noemi
Merci madame maintenant on demande de considerer lim $U_n-U_{n+1} =0$ comme un taux d'accroissement afin de demontre que la reciproque est fausse !

@loicstephan

Etudie $U_{n+1}-U_n$ pour la suite $U_n=ln(n)$ .

Bonjour,

Je suis perplexe...

@loicstephan , Noemi t'a donné des réponses indentiques à celle du lien que je t'indique ici :
Exercice 1 questions 3 et 4 :
https://jfresan.files.wordpress.com/2011/10/feuille1-annee-11-12.pdf

Mais sur ce site les questions sont :
3 : Prouver que si $U_n)$ converge, alors $U_{n+1}-U_n$ tend vers 0 quand n tend vers $+∞+\infty$
4 : Contre exemple donné $U_n=ln(n)$ , pour prouver que la réciproque est fausse, c'est à dire que lorsque $U_{n+1}-U_n$ tend vers 0 quand n tend vers $+∞+\infty$ , on peut avoir une suite $U_n)$ non convergente.

Ces questions/réponses correspondent-t-elles exactement à ton énoncé ? ? ?

Pour le savoir, si tu le souhaites, je te conseille d'écrire ton énoncé , non comme tu le comprends, mais, à la lettre près, comme il t'a été donné, pour lever toute confusion éventuelle.

@mtschoon
bonjour

Montrer que si $u_n)$ converge alors $lim⁡n→+∞un+1−un=0\displaystyle \lim_{n\to+\infty} u_{n+1} − u_n = 0$
Montrer que la réciproque est fausse.
Interpréter $u_{n+1} − u_n$ comme un taux d’accroissement afin de trouver un contre-exemple.

voici en effet l'intitule exacte de mon exercice !

@loicstephan , re-bonjour,

Merci pour l'intitulé exact de ton exercice.
Cette fois, c'est clair.
Une autre fois, je te conseille de donner l'intitulé exact depuis le début.

Pour la question 1. c'est bon, tu as tout ce qu'il faut.

Pour la 2), l'énoncé te donne une piste pour t'aider à trouver un contre-exemple car ce n'est pas évident ...

J'explicite un peu cette aide proposée par ton énoncé

Soit f une fonction définie pour $x≥0x\ge 0$ ou $x>0x\gt 0$

Tu peux poser : $f(n)=U_n ; f(n+1)=U_{n+1}$
Donc :
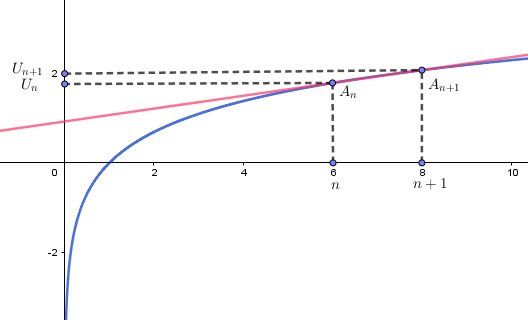
$Un+1−Un=f(n+1)−f(n)=f(n+1)−f(n)(n+1)−nU_{n+1}-U_n=f(n+1)-f(n)=\dfrac{f(n+1)-f(n)}{(n+1)-n}$
$U_{n+1}-U_n$ est donc le taux d'accoissement de la fonction f entre les points $A_n(n, f(n))$ et $A_{n+1}(n+1,f(n+1))$ de la représentation graphique de f
(Ce taux d'accroissement est le coefficient directeur de la droite $A_nA_{n+1})$

Losrque n tend vers $+∞+\infty$ , ce taux d'accroissement tend vers 0.
La courbe doit devenir "presque" parallèle à l'axe des abscisses.
La fonction f que l'on cherche doit donc avoir, , lorsque x tend vers $+∞+\infty$ , l'axe des abscisses pour direction asymptotique.

Quelles fonctions f usuelles admettant l'axe des abscisses comme direction asymptotique en $+∞+\infty$ ?

Tu as le choix.

Il y a la fonction logarithme népérien .
donc tu peux poser $f(x)=ln(x)\boxed{f(x)=ln(x)}$ et utiliser cette fonction pour le contre exemple comme indiqué (les calculs sont faits dans le lien donné)

Il y a aussi la fonction racine carrée
donc tu peux poser, si tu préfères, $f(x)=x\boxed{f(x)=\sqrt x}$ et utiliser cette fonction pour le contre exemple.

Il y en a bien d'autres...

Reposte si mon explication n'est pas claire.

Illustration graphique (pour la réciproque) avec la fonction ln