Exercice en rapport avec continuité et derivation

[Quentinply]

Bonsoir à tous je suis bloqué sur cet exo pouvez vous m'aidez?
Pour tout entier n>= , on considère la fonction fn définie sur [0;1] par fn (x) = x³-2nx+1.

1. Dresser le tableau de variation de fn.
2. Démontrer que pour tout entier naturel n>= 2, l'équation fn(x)=0 admet une unique solution, que l'on notera alpha,n dans [0;1]
   Merci de votre aide

[Noemi]

@Quentinply Bonsoir, (Marque de politesse à ne pas oublier !!)

Il manque une indication pour $n$;
Calcule la dérivée de la fonction et étudie son signe pour dresser le tableau de variation.

[mtschoon]

Bonjour,

@Quentinply , je te donne quelques indications pour le cas où $n\ge 2$ , sur l'intervalle [0,1]

$f_n(x)=x^3-2nx+1$
$f_n^{\prime }(x)=3x^2-2n$

Sur $R$,
$f_n^{\prime }(x)=0$<=> $x=-\sqrt{\frac{2n}{3}}$ et $x=+\sqrt{\frac{2n}{3}}$
$f_n^{\prime }(x)>0$<=> $x\in ]-\infty ,-\sqrt{\frac{2n}{3}}[\cup ]\sqrt{\frac{2n}{3}},+\infty [$
$f_n^{\prime }(x)<0$<=> $x\in ]-\sqrt{\frac{2n}{3}},\sqrt{\frac{2n}{3}}[$

Vu que $n\ge 2$, $\sqrt{\frac{2n}{3}}>1$
donc : $[0,1]\subset ]-\sqrt{\frac{2n}{3}},\sqrt{\frac{2n}{3}}[$ , donc $f_n^{\prime }(x)<0$ pour $x\in [0,1]$

De plus , $f_n(0)=1$ et $f_n(1)=2(1-n)$
Vu que $n\ge 2$, $f_n(1)<0$

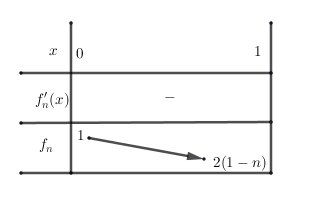
$f_n$ est définie dérivable donc continue et strictement décroissante donc bijective de $[0,1]$ vers $[2(1-n),1]$

$0\in [2(1-n),1]$ donc 0 a un antécédent unique ${\alpha }_n$ dans [0,1]

L'équation $f_n(x)=0$ admet une unique solution ${\alpha }_n$ dans [0,1]

Remarque : il y a ici le plan du travail, mais tous les calculs sont à faire et les explications à donner

[mtschoon]

Bonjour,

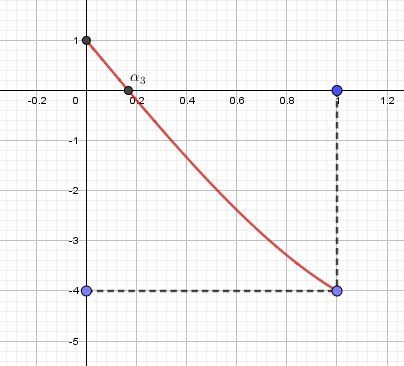
Représentation graphique pour $n=3$ : $f_3(x)=x^3-6x+1$

${\alpha }_3\approx 0.167$ car
$f(0.167)\approx 0.00266$ et $f(0.168)\approx -0.0033$