suites et etude des tumeurs
-
Lloicstephan dernière édition par Noemi
bonjour chaleureux a tous !
On observe une tumeur : certaines cellules sont saines mais d’autres sont malades. Un
traitement permet de transformer chaque jour une certaine proportion ppp des cellules malades en cellules saines. Malheureusement, une certaine proportion qqq des cellules malades devient résistante au traitement. Une proportion rrr des cellules malades n’est pas touchée par le traitement, et reste malade.
On va étudier, en fonction du nombre n de jours de traitement, l’évolution des proportions de
cellules saines (an)(a_n)(an), malades (bn)(b_n)(bn) et malades resistantes (cn)(c_n)(cn).
On pose par exemple a0=0,99a_0 = 0, 99a0=0,99, b0=0,009b_0 = 0, 009b0=0,009 et c0=0,001c_0 = 0, 001c0=0,001.- Que vaut p+q+rp + q + r p+q+r ? an+bn+cna_n + b_n + c_nan+bn+cn ?
- On suppose dans la suite que p=0,1p = 0, 1p=0,1 et q=0,01q = 0, 01q=0,01
(a) Exprimer an+1a_{n+1}an+1, bn+1b_{n+1}bn+1 et cn+1c_{n+1}cn+1 en fonction de ana_nan, bnb_nbn et cnc_ncn.
(b) Observer l’évolution (variations, limites, vitesse de convergence...) des trois suites
grâce à un tableur.
(c) Montrer que (bn)(b_n)(bn) est géométrique.
(d) En déduire son terme général puis ceux de (an)(a_n)(an) et (cn)(c_n)(cn).
(e) Déterminer les limites de ces trois suites.
(f) Vérifier ces résultats sur la feuille de calcul du tableur. - Combien de jours sont nécessaires à une stabilisation de la proportion de cellules saines
au millième près ? - Que peut-on conclure sur l’efficacité du traitement (points positifs et négatifs)
je ne peux demarrer l'exercice car je ne saisie meme pas la question 1
merci!!!
-
@loicstephan Bonjour,
Exprime a1a_1a1, b1b_1b1,c1c_1c1 en fonction de a0a_0a0, b0b_0b0, c0c_0c0, ppp, qqq et rrr.
Tu en déduis la première relation.
Puis ana_nan,bnb_nbn et cnc_ncn.
pour la deuxième relation.
-
Lloicstephan dernière édition par
@Noemi
ce qui m'mbete ce n'est pas l'expression de mis ce que represente repectivement p,q,rp,q,rp,q,r
sont elle les differentes raisons des suites?
-
Lloicstephan dernière édition par
@loicstephan si oui comment car a la lecture de l'exercices l'information ne ressot fondanmentalement pas!
-
Ceux sont des proportions, donc un coefficient, pas les raisons.
a1=a0+p×b0a_1=a_0+p\times b_0a1=a0+p×b0
b1=....b_1=....b1=....
c1=....c_1=....c1=....
-
mtschoon dernière édition par mtschoon

Bonjour,
Personnellement, je trouve cet énoncé difficile à déchiffrer, car on peut s'égarer entre ces différentes proportions...
J'ai tenté un schéma pour y voir plus clair.
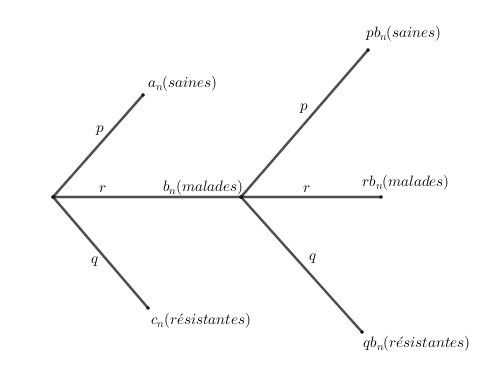
p,q,rp,q,rp,q,r étant les proportions des transformations effectuées chaque jour, je dirais : p+q+r=1p+q+r=1p+q+r=1
an,b,cna_n,b_,c_nan,b,cn étant les proportions des cellules (saines, malades, résistantes) chaque jour, je dirais :
an+bn+cn=1a_n+b_n+c_n=1an+bn+cn=1Dans le schéma, an,bn,cna_n, b_n, c_nan,bn,cn sont les proportions le jour nnn
Le jour suivant, c'est à dire le jour(n+1)(n+1)(n+1), ce sont les cellules malades (proportion bnb_nbn) qui sont transformées en saines, malades, résistantes, avec les proportions p,r,qp,r,qp,r,q, les saines et résistantes du jour nnn ne changeant pas.
Bilan des proportions des cellules le jour (n+1)(n+1)(n+1) :
pour les cellules saines : an+1=pbn+ana_{n+1}=pb_n+a_nan+1=pbn+an
pour les cellules malades : bn+1=rbnb_{n+1}=rb_nbn+1=rbn
pour les cellules résistantes : cn+1=qbn+cnc_{n+1}=qb_n+c_ncn+1=qbn+cnVérifications:
an+1+bn+1+cn+1=pbn+an+rbn+qbn+cna_{n+1}+b_{n+1}+c_{n+1}=pb_n+a_n+rb_n+qb_n+c_nan+1+bn+1+cn+1=pbn+an+rbn+qbn+cn
an+1+bn+1+cn+1=bn(p+q+r)+an+cn=bn(1)+an+cna_{n+1}+b_{n+1}+c_{n+1}=b_n(p+q+r)+a_n+c_n=b_n(1)+a_n+c_nan+1+bn+1+cn+1=bn(p+q+r)+an+cn=bn(1)+an+cn d'où
an+1+bn+1+cn+1=bn+an+cn=1a_{n+1}+b_{n+1}+c_{n+1}=b_n+a_n+c_n=1an+1+bn+1+cn+1=bn+an+cn=1
c'est bon.Voilà ce que j'ai compris avec cet énoncé...
Bon courage @loicstephan !
-
mtschoon dernière édition par mtschoon

Bonjour,
Quelques indications pour trouver les expressions de an,bn,cna_n,b_n,c_nan,bn,cn, si besoin.
bn+1=rbnb_{n+1}=rb_nbn+1=rbn donc (bn)(b_n)(bn) est la suite géométrique de premier terme b0b_0b0 et de raison rrr donc :
bn=born\boxed{b_n=b_or^n}bn=bornPour ana_nan et cnc_ncn penser à des sommes télescopiques.
an+1=an+pbna_{n+1}=a_n+pb_nan+1=an+pbn
on applique cette formule de ana_nan à a1a_1a1 :
{an=an−1+pbn−1an−1=an−2+pbn−2an−2=an−3+pbn−3......a2=a1+pb1a1=a0+pb0\begin{cases} a_{n}=a_{n-1}+pb_{n-1}\cr a_{n-1}=a_{n-2}+pb_{n-2}\cr a_{n-2}=a_{n-3}+pb_{n-3}\cr ...\cr ...\cr a_{2}=a_1+pb_1\cr a_{1}=a_0+pb_0 \end{cases}⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧an=an−1+pbn−1an−1=an−2+pbn−2an−2=an−3+pbn−3......a2=a1+pb1a1=a0+pb0En ajoutant les membres de gauche ensemble et les membres de droite ensemble et après simplifications :
{an=an−1+pbn−1an−1=an−2+pbn−2an−2=an−3+pbn−3......a2=a1+pb1a1=a0+pb0\begin{cases} a_{n}=\sout {a_{n-1}}+pb_{n-1}\cr \sout{a_{n-1}}=\sout{a_{n-2}}+pb_{n-2} \cr \sout{a_{n-2}} =\sout{a_{n-3}}+pb_{n-3}\cr \sout{...}\cr \sout{...}\cr \sout{a_{2}}=\sout{a_1}+pb_1\cr \sout{a_{1}}=a_0+pb_0 \end{cases}⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧an=an−1+pbn−1an−1=an−2+pbn−2an−2=an−3+pbn−3......a2=a1+pb1a1=a0+pb0Il reste
an=a0+p(bn−1+bn−2−bn+3+...+...+b1+b0)a_n=a_0+p(b_{n-1}+b_{n-2}-b_{n+3}+...+...+b_1+b_0)an=a0+p(bn−1+bn−2−bn+3+...+...+b1+b0)bn−1+bn−2−bn+3+...+...+b1+b0b_{n-1}+b_{n-2}-b_{n+3}+...+...+b_1+b_0bn−1+bn−2−bn+3+...+...+b1+b0 est la somme des n premiers termes de la suite géométrique de premier terme b0b_0b0 et de raison rrr.
Donc :
bn−1+bn−2−bn+3+...+...+b1+b0=b0×1−rn1−rb_{n-1}+b_{n-2}-b_{n+3}+...+...+b_1+b_0=b_0\times \dfrac{1-r^n}{1-r}bn−1+bn−2−bn+3+...+...+b1+b0=b0×1−r1−rnAu final :
an=a0+pb0(1−rn1−r)\boxed{a_n=a_0+pb_0\biggr(\dfrac{1-r^n}{1-r}\biggr)}an=a0+pb0(1−r1−rn)Le calcul de cnc_ncn se fait de la même façon.
Bonne lecture éventuelle.