Math expert cosinus et sinus
-
RRK dernière édition par
Bonjour pouvez-vous m’aider svp
Soit x un nombre réel.- En écrivant que 3x= 2x+x, démontrer que :
cos(3x)= 4cos^3 (x)-3cos(x). - Prouver de même que :
sin(3x)=-4sin^3(x)+3sin(x). - a. En déduire que cos(pie/9) est solution de l'équation : 4x^3 - 3x- =0.
b. Démontrer que cette équation a exactement trois solutions dans R.
c. À l'aide de la çalculatrice, trouver une valeur appro- chée à 10^-3 de cos(pie/9) - Trouver une valeur approchée à 10^-3 de sin(pie/9)
mercii
Pour la première question j’ai commencer en utilisant les formules de duplication.
Cos (3x)= cos (2x+x)
= cos(2x) * cos(x) - sin (2x)* sin(x)
=2cos^2(x)-1*cos(x)-2sin(x)*cos(x)*sin(x)
= 2cos^3 (x) -1 -2sin^2 (x) * cos(x)
Et la je bloque si vous pouvez m’aider svppp Mercii
- En écrivant que 3x= 2x+x, démontrer que :
-
mtschoon dernière édition par mtschoon

@RK , bonjour,
Tes expressions manquent de parenthèses...il faudra les compléter sur ta copie...
Pour terminer ta première question, remplace sin2(x)sin^2(x)sin2(x) par 1−cos2(x)1-cos^2(x)1−cos2(x) vu que tu connais la formule fondamentale :
sin2(x)+cos2(x)=1sin^2(x)+cos^2(x)=1sin2(x)+cos2(x)=1Applique le même principe pour la question 2.
Pour la 3a), pense à poser x=π9x=\dfrac{\pi}{9}x=9π et à utiliser la formule trouvée pour cos(3x)cos(3x)cos(3x)
Remarque : l'équation que tu donnes est incomplète.
Reposte si besoin.
-
RRK dernière édition par
@mtschoon
Donc
Cos (3x)= cos (2x+x)
= cos(2x) * cos(x) - sin (2x)* sin(x)
=2cos^2(x)-1*cos(x)-2sin(x)*cos(x)*sin(x)
= 2cos^3 (x) -1 -2sin^2 (x) * cos(x)
= 2 cos^3(x)-1-(2-2cos^2(x) cos(x))
= 2 cos^3(x)-1-2+2cos^2(x) cos(x))
= 2 cos^3(x)-3 +2cos^2(x) cos(x))
= ??
Et pour l’équation oui j’ai oublié de finir c’est 4x^3-3x-1/2=0
-
@RK Bonjour,
Il manque des parenthèses ou crochets
cos(2x)cos(x)−sin(2x)sin(x)=cos(2x)cos(x)-sin(2x)sin(x)=cos(2x)cos(x)−sin(2x)sin(x)=
[2cos2(x)−1]cos(x)−2sin2(x)cos(x)=[2cos^2(x)-1]cos(x)-2sin^2(x)cos(x)= [2cos2(x)−1]cos(x)−2sin2(x)cos(x)=
2cos3(x)−cos(x)−2[1−cos2(x)]cos(x)=2cos^3(x)-cos(x)-2[1-cos^2(x)]cos(x)=2cos3(x)−cos(x)−2[1−cos2(x)]cos(x)=
2cos3(x)−cos(x)−2cos(x)+2cos3(x)=.....2cos^3(x)-cos(x)-2cos(x)+2cos^3(x)= .....2cos3(x)−cos(x)−2cos(x)+2cos3(x)=.....
-
RRK dernière édition par
@Noemi
Merciii
cos(2x)cos(x)−sin(2x)sin(x)=
[2cos2(x)−1]cos(x)−2sin2(x)cos(x)=[2cos^2(x)-1]cos(x)-2sin^2(x)cos(x)= [2cos
2(x)−1]cos(x)−2sin
2
(x)cos(x)=
2cos3(x)−cos(x)−2[1−cos2(x)]cos(x)=2cos^3(x)-cos(x)-2[1-cos^2(x)]cos(x)=2cos
3
(x)−cos(x)−2[1−cos
2
(x)]cos(x)=
2cos3(x)−cos(x)−2cos(x)+2cos3(x)=.....2cos^3(x)-cos(x)-2cos(x)+2cos^3(x)= .....2cos
3
(x)−cos(x)−2cos(x)+2cos
3
(x)= 4cos^4(x)-3cos(x)
-
RRK dernière édition par
@RK
C’est bon j’ai réussi la question 2
Pouvez-vous me donner des indications pour la 3a svp
-
mtschoon dernière édition par mtschoon

@RK , je t'ai déjà donné des pistes pour la 3)a)
Revois ma réponse.
Tu sais que cos(3x)=4cos3(x)−3cos(x)cos(3x)=4cos^3(x)-3cos(x)cos(3x)=4cos3(x)−3cos(x)
Tu choisis x=π9x=\dfrac{\pi}{9}x=9π, d'où :
cos(π3)cos(\dfrac{\pi}{3})cos(3π)=4cos3(π9)−3cos(π9)4cos^3(\dfrac{\pi}{9})-3cos(\dfrac{\pi}{9})4cos3(9π)−3cos(9π)
Tu sais que cos(π3)=12cos(\dfrac{\pi}{3})=\dfrac{1}{2}cos(3π)=21, d'où
4cos3(π9)−3cos(π9)=124cos^3(\dfrac{\pi}{9})-3cos(\dfrac{\pi}{9})=\dfrac{1}{2}4cos3(9π)−3cos(9π)=21
4cos3(π9)−3cos(π9)−12=04cos^3(\dfrac{\pi}{9})-3cos(\dfrac{\pi}{9})-\dfrac{1}{2}=04cos3(9π)−3cos(9π)−21=0
conclusion :
cos(π9)cos(\dfrac{\pi}{9})cos(9π) est solution de : 4x3−3x−12=04x^3-3x-\dfrac{1}{2}=04x3−3x−21=0
Revois tout ça et essaie de poursuivre.
-
RRK dernière édition par
@mtschoon
Merci beaucoup j’ai compris
-
mtschoon dernière édition par mtschoon

@RK , c'est bien.
Je te donne une piste pour la 3)b)
Tu peux poser f(x)=4x3−3x−12f(x)=4x^3-3x-\dfrac{1}{2}f(x)=4x3−3x−21
Tu étudies les variations de f.
Avec le TVI (utilisé sur 3 intervalles) , tu pourras prouver que l'équation a 3 solutions, c'est à dire qu'il y a 3 valeurs réelles de x telles que f(x)=0f(x)=0f(x)=0
-
RRK dernière édition par
@mtschoon
F’(x)=12x^2-3
12x^2-3 >0
Donc f est croissante
-
mtschoon dernière édition par mtschoon

@RK ,
Oui pour f′(x)=12x2−3f'(x)=12x^2-3f′(x)=12x2−3 mais Non pour f′(x)>0f'(x)\gt 0f′(x)>0
Tu peux factoriser f′(x)f'(x)f′(x)
f′(x)=3(4x2−1)=3(2x−1)(2x+1)f'(x)=3(4x^2-1)=3(2x-1)(2x+1)f′(x)=3(4x2−1)=3(2x−1)(2x+1)f′(x)=0f'(x)=0f′(x)=0 <=> 2x−1=02x-1=02x−1=0 ou 2x+1=02x+1=02x+1=0 <=> x=12x=\dfrac{1}{2}x=21 ou x=−12x=-\dfrac{1}{2}x=−21
Tu continues.
-
mtschoon dernière édition par mtschoon

@RK ,
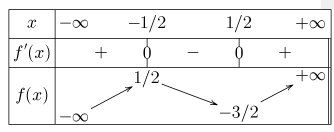
Voici le tableau de variation que tu dois trouver.
Tout est à prouver, bien sûr ! ! !
-
mtschoon dernière édition par

Illustration graphique.
xA,xB,xCx_A,x_B,x_CxA,xB,xC sont les solutions de f(x)=0f(x)=0f(x)=0
xA<0x_A\lt 0xA<0, xB<0x_B\lt 0xB<0, xC>0x_C\gt0xC>0
Vu que cos(π9)>0cos(\dfrac{\pi}{9})\gt 0cos(9π)>0 , on déduit cos(π9)=xCcos(\dfrac{\pi}{9})=x_Ccos(9π)=xC
A la calculette : xC≈0.934x_C\approx 0.934xC≈0.934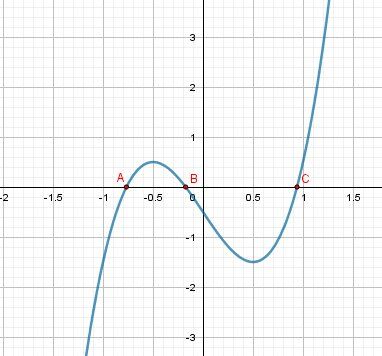
-
RRK dernière édition par
-
RRK dernière édition par
@mtschoon
Mercii
Jài réussi à trouver les mêmes réponses
Et après il fait que j’utilise le TVI ?
Si oui je met
Sur ]-infinie;+infinie[ f est continue et f est croissante sur l’intervalle -infinie -1/2 ouvert
f est décroissante sur l’intervalle -1/2;1/2 ouvert et
f est croissante sur 1/2;+infinie ouvert
-
RRK dernière édition par
@RK
Alpha 1 appartient a -infinie; 1/2
Alpha 2 appartient a 1/2;-3/2
Alpha 3 appartient a -3/2 ; +infinie
Les trois intervalles ouvert
Donc d’après le TVI, l’équation admet trois solution alpha 1, alpha 2, alpha 3 sur -infinie; +infinie ouvert.
-
mtschoon dernière édition par mtschoon

@RK ,
Oui, c'est bon, à condition de préciser "strictement croissante", "strictement décroissante" , pour justifier l'unicité de chaque solution par intervalle.
-
RRK dernière édition par
@mtschoon
D’accord
Merci beaucoup
-
mtschoon dernière édition par

De rien @RK et bon travail .