Exercice Second degré
-
CChachap dernière édition par
Bonjour ! J’ai besoin d’aide sur un exercice, je vois vraiment pas comment le résoudre, merci pour ceux qui m’aideront:
Dans un repère orthonormé, on donne les points A(0;-2) et B(3;2). M est un point de l’axe des abscisses.
Déterminer les positions du point M tel que le triangle ABM soit rectangle en M.
-
@Chachap Bonjour,
Soit M(x;0)M(x;0)M(x;0), exprime les distances AMAMAM et BMBMBM en fonction de xxx, puis utilise le théorème de Pythagore.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Chachap , je te mets une illustration graphique pour te permettre de vérifier tes résultats.Le triangle ABM doit être rectangle en M, donc M doit être sur le cercle de diamètre [AB]
M doit aussi être sur l'axe des abscisses
Donc M doit être à l'intersection du cercle et de l'axe des abscisses.
Tu trouveras donc, après calculs, deux points M notés M1M_1M1 etM2M_2M2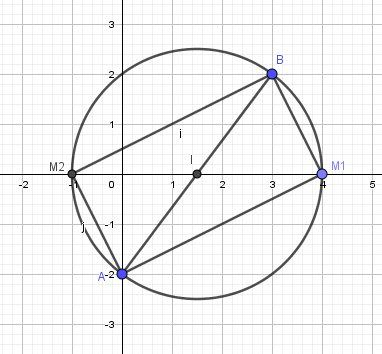
SI tu sais trouver l'équation d'un cercle, tu peux l'utiliser pour répondre à la question posée.
Tu as le choix !
-
mtschoon dernière édition par mtschoon

Bonjour,
@Chachap, je mets quelques pistes pour résoudre le problème avec le cercle.
I milieu de [AB]
xI=xA+xB2=32x_I=\dfrac{x_A+x_B}{2}=\dfrac{3}{2}xI=2xA+xB=23
yI=yA+yB2=0y_I=\dfrac{y_A+y_B}{2}=0yI=2yA+yB=0
Soit RRR le rayon du cercle.
R=IA=(xA−xI)2+(yA−yI)2=52R=IA=\sqrt{(x_A-x_I)^2+(y_A-y_I)^2}=\dfrac{5}{2}R=IA=(xA−xI)2+(yA−yI)2=25
Equation du cercle :
(x−xI)2+(y−yI)2=R2(x-x_I)^2+(y-y_I)^2=R^2(x−xI)2+(y−yI)2=R2
(x−32)2+(y−0)2=254(x-\dfrac{3}{2})^2+(y-0)^2=\dfrac{25}{4}(x−23)2+(y−0)2=425
Vu que les points M sont sur l'axe des abscisses : y=0y=0y=0D'où :(x−32)2=254(x-\dfrac{3}{2})^2=\dfrac{25}{4}(x−23)2=425
(x−32)2−(52)2=0(x-\dfrac{3}{2})^2-(\dfrac{5}{2})^2=0(x−23)2−(25)2=0
On termine pour trouver les deux valeurs de x solutions.Tu peux faire, si tu préfères la méthode avec le théorème de Pythagore :
MA2+MB2=AB2MA^2+MB^2=AB^2MA2+MB2=AB2L'idéal, pour t'entraîner est de faire les deux et t'assurer que tu trouves pareil.
Bons calculs.