Fonction réciproque bijection
-
Baraa Skhairi 0 dernière édition par
Bonsoir
Comment je peut déterminer (g-1)' pour tout x dans]-2,0[
j'ai appliqué la règle mais j'ai été bloqué
g(x) =cos(pi x) ; x dans [0,1]
-
@Baraa-Skhairi-0 Bonjour,
-
Baraa Skhairi 0 dernière édition par
@Noemi
C'était un peu compliqué
-
Quelle règle appliques-tu ?
Indique tes calculs ou questions.
Les fonctions sinusoïdales sont des cas particuliers.
-
Baraa Skhairi 0 dernière édition par
@Noemi
1/ g'(g^-1)
-
mtschoon dernière édition par mtschoon

Bonjour,
@Baraa-Skhairi-0 , je comprends guère à quel intervalle appartient x car je vois ]-2,0[ et [0,1]...
Je prends [0,1] et g(x)=cos(πx)g(x)=cos(\pi x)g(x)=cos(πx)
Sur cette intervalle, en étudiant g, tu dois trouver que g est une bijection de [0,1] vers [-1,1]
g admet donc une bijection réciproque g−1g^{-1}g−1 de [-1,1] vers [0,1]Graphique :
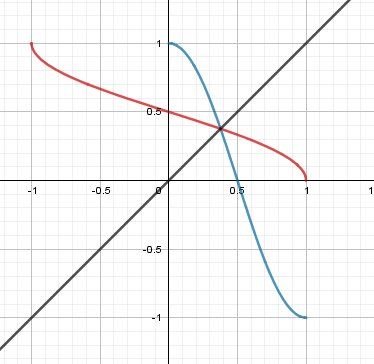
la représentation graphique de la fonction ggg est en bleu
la représentation graphique de la fonction g−1g^{-1}g−1 est en rouge
Ces deux représentations graphiques, en repère orthonormé, sont symétriques par rapport à la droite y=x (en noir)Expression de g−1(x)g^{-1}(x)g−1(x)
y=cos(πx)y=cos(\pi x)y=cos(πx)
en échangeant le rôle de x et de y
x=cos(πy)x=cos(\pi y)x=cos(πy)
cos(πy)=xcos(\pi y)=xcos(πy)=x
πy=arccos(x)\pi y=arccos(x)πy=arccos(x)
y=arccos(x)πy=\dfrac{arccos(x)}{\pi}y=πarccos(x)
donc g−1(x)=arccos(x)πg^{-1}(x)=\dfrac{arccos(x)}{\pi}g−1(x)=πarccos(x)
-
mtschoon dernière édition par mtschoon

Pour la dérivée de g−1g^{-1}g−1, si tu connais la dérivée de arccos, tu l'utilises directement.
(arccos(x))′=−11−x2(arccos(x))'=\dfrac{-1}{\sqrt{1-x^2}}(arccos(x))′=1−x2−1
donc (g−1)′(x)=−1π1−x2(g^{-1})' (x)=\dfrac{-1}{\pi\sqrt{1-x^2}}(g−1)′(x)=π1−x2−1
Si tu ne le sais pas, il faut le prouver.
Il y a la démonstration détaillée ici :
https://www.math-linux.com/mathematiques/derivee-de-fonction/article/derivee-de-arccos-x
J'espère que ça t'ira...
Bons calculs.