Nombres complexes Ex 1

Bonjour,Pouvez vous m'aider à resoudre cet exercice svp

Résoudre et représenter les solutions dans le plan de Gauss :
𝑧*4−𝑖+1=0

Je ne sais pas par ou commencer !

@Joyca2 Bonjour,

Je suppose que l'équation est $z^4-i+1=0$
Une piste, tu poses $Z=z^2$ , puis tu commences par résoudre
$Z^2=-1+i$

Bonjour,

Alternative :

Je présume qu'il s'agit de z^4 - i + 1 = 0

z^4 = -1 + i
z^4 = V2 * (-1/V2 + i.1/V2) (avec V pour racine carrée)

z^4 = V2 * e^(i.(3Pi/4 + 2k.Pi))

z = (V2)^(1/4) * e^(i.(3Pi/4 + 2k.Pi)/4)

z = 2^(1/8) * (cos(3Pi/16 + k.Pi/2) + i.sin(3Pi/16 + k.Pi/2))

avec k = 0, 1 , 2 ou 4

@Noemi Vu que c'est du second dégré j'ai utilisé delta : j'ai trouve -5 que j'ai mis sous forme de complexe ce qui m'a donné 5i*2 Est ce correct ?

@Black-Jack Bonjour merci ,j'aimerais juste savoir comment le representer dans le plan de Gauss,dois je donner une echelle ?

@Joyca2

Vérifie tes calculs pour delta.

@Joyca2

z = 2^(1/8) * (cos(3Pi/16 + k.Pi/2) + i.sin(3Pi/16 + k.Pi/2))

k = 0 --> z0 = 2^(1/8) * (cos(3Pi/16) + i.sin(3Pi/16))
et à la calculette, on trouve (en arrondissant les parties rélle et imaginaire) : zo = 0,906724 + 0,605854.i

k = 1 --> z1 = 2^(1/8) * (cos(3Pi/16 + Pi/2) + i.sin(3Pi/16 + Pi/2))
et à la calculette, on trouve (en arrondissant les parties rélle et imaginaire) : z1 = - 0,605854 + 0,906724.i

k = 2
...

k = 3
...

Facile alors de positionner les points d'affixe z0, z1 , z2 et z3 dans le plan complexe (aussi appelé plan d'Argand, plan d'Argand-Cauchy ou plan d'Argand-Gauss).
... qui devra évidemment avoir des axes gradués.

Remarque, il est possible d'obtenir les expressions exactes (avec radicaux) de z0, z1, z2 et z3 (mais ce n'est pas demandé)

En remarquant que 3Pi/16 est l'angle moitié de 3Pi/8 qui est l'angle moitié de 3Pi/4 ... dont on connait les sinus et cosinus, et donc ...

Tu dois évidemment arriver aux mêmes solutions en suivant la piste donnée par Noemi

Bonjour,

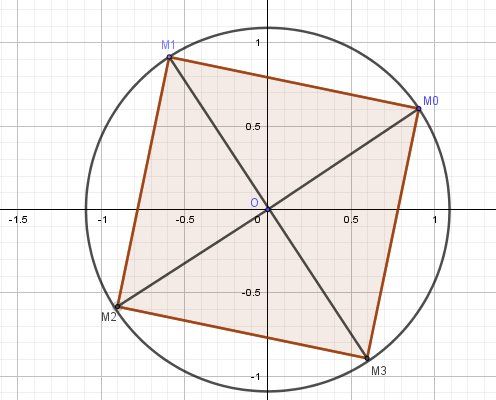
@Joyca2, je te mets la représentation graphique des solutions de l'équation $z^4=-1+i$ obtenues avec les racines 4èmes de $(- 1 + i)$ , c'est à dire $z=2(18)e(3iπ16+kπ2)z=2^{(\dfrac{1}{8})}e^{(\dfrac{3i\pi}{16}+\dfrac{k\pi}{2})}$
(k prenant les valeurs 0,1,2,3)

On trace le cercle de centre O et de rayon $2182^\dfrac{1}{8}$

Sur ce cercle, on place l'image M0 pour $k = 0$ et les autres images M1,M2,M3 se déduisent directement (en formant un carré ).

Bien sûr, tu peux aussi utiliser la voie algébrique pour résoudre l'équation.
Pour cela, suis la piste de @Noemi.

@Noemi en verifions j'ai trouver 3i*2 est-ce correct cet fois-ci ?

@Black-Jack Est-on obliger de le mettre sous forme décimale ou on peut aussi le représenter avec des radians?

@Joyca2 a dit dans Nombres complexes Ex 1 :

@Black-Jack Est-on obliger de le mettre sous forme décimale ou on peut aussi le représenter avec des radians?

C'est à toi de savoir ce que ton prof attend.

Pour placer les 4 points solutions dans le plan complexe, on peut aussi faire comme montré sur le dessin de mtschoon.

Dans les 2 cas, c'est quand même un dessin "à peu près" si on le trace sans logiciel ad hoc.
Placer par exemple un point d'affixe zo = 0,906724 + 0,605854.i alors que 0,906724 et 0,605854 sont déjà des arrondis et aller mesurer cela "à la latte" pour les placer sur le dessin du plan est imprécis.

Mais dessiner un cercle de rayon 2^(1/8) sur un papier n'est pas non plus très précis si on tente de graduer les axes du repère par unités.

Mais cela n' a pas grande importance.

@Black-Jack ok et moi quand je dois le tracer,dois je preciser une echelle car le prof n'a rien precise à ce sujet !

@Joyca2 a dit dans Nombres complexes Ex 1 :

@Black-Jack ok et moi quand je dois le tracer,dois je preciser une echelle car le prof n'a rien precise à ce sujet !

L'échelle est d'office connue par les repères gradués sur les axes du dessin.

@Joyca2 , pour information,

Pour faire le graphique joint, j'ai tout simplement utilisé "geogébra" en lui indiquant $2182^\dfrac{1}{8}$ et $3π16\dfrac{3\pi}{16}$ , c'est à dire pour M0 :
les coordonnées $(218cos(3π16),218sin(3π16)\biggr(2^\dfrac{1}{8}cos(\dfrac{3\pi}{16}), 2^\dfrac{1}{8}sin(\dfrac{3\pi}{16}\biggr)$ et le logiciel fait le job !

Sur papier, tu fais au mieux avec règle graduée, compas, rapporteur, mais dans les calculs ne parle que des valeurs exactes ( $2182^\dfrac{1}{8}$ pour le module et mesures en radians pour les arguments).