Nombres complexe Ex2

Bonjour, Pouvez-vous m'aider à résoudre cet exercice svp
Résoudre : 𝑧°6+(1−2𝑖)𝑧°3−2𝑖=0

@Joyca2 Bonjour,

Une piste :
Poser $Z= z^3$
résoudre l'équation du second degré, puis déterminer $z$ .

Indique tes calculs et/ou réponse si tu souhaites une vérification.

Bonjour,

@Joyca2 , je t'avance un peu le travail

En posant $z^3=Z$ , tu dois commencer par résoudre l'équation auxiliaire $Z^2+(1-2i)Z-2i=0$

Avant de passer par le discriminant (et peut-être d'éviter d'y passer), je te conseille de chercher d'abord une solution dite "évidente".
Traditionnellement, on cherche si +1,-1,+i ,-i ne seraient pas une solution de l'équation.

Ici, tu dois trouver que $Z = - 1$ est solution.

Dans une équation du second degré de la forme $aZ^2+bZ+c=0$ , le produit des solutions vaut $ca\dfrac{c}{a}$

Donc $Z_1Z_2=-2i$

Vu que $Z_1=-1$ , tu peux déduire $Z_2$

Essaie de poursuivre.

@mtschoon Bonjour,je ne vois vraiment pas comment vous avez pu obtenir Z = -1 ,Pouvez-vous detaillez votre calcul svp?

@mtschoon j'ai trouver que Z2 = 2i Est-ce correct ?

@Joyca2 Bonjour,

$Z_2=2i$ est correct.
Pour $Z_1=-1$
remplace $Z$ par $- 1$ dans l'équation :
$Z^2+(1-2i)Z-2i=0$

@Joyca2 ,
Calcul pour Z=-1 : $1)^2+(1-2i)(-1)-2i=0$ <=> $1 - 1 + 2 i - 2 i = 0$

Tu as maintenant les deux solutions de l'équation d'inconnue $Z$ qui sont $- 1$ et $2 i$

Il faut revenir à $z$ en résolvant $z^3=-1$ et $z^3=2i$

Pour cela, je te conseille d'utiliser ton cours sur les racines cubiques (racines nièmes, de façon générale) .

@mtschoon j'ai trouver 3 solutions : Z0 = -1 ,Z1 = e°5ipi/3 et Z2 = e°ipi/3 Est ce correct ?

@Joyca2 ,

Si tu parles de l'équation $z^3=-1$ c'est bon.

Les 3 solutions sont bien -1, $eiπ3e^{\dfrac{i\pi}{3}}$ et $e5iπ3e^{\dfrac{5i\pi}{3}}$

Maintenant, il te reste à résoudre $z^3=2i$

@mtschoon j'aimerais bien mais on ne peut pas mettre 2i sous forme d'un niemes cubiques ! Je suis bloqué

@Joyca2 ,

Tu appliques la méthode usuelle en mettant 2i sous forme exponnentielle.
$2i=eiπ22i=e^{\dfrac{i\pi}{2}}$ et tu résous $z3=2eiπ2z^3=2e^{\dfrac{i\pi}{2}}$ c'est à dire $z$ racine cubique de $2eiπ22e^{\dfrac{i\pi}{2}}$

@mtschoon finalement,on vient de trouver z qui egale à la racine cubique de 2e*ipi/2

C'est ca non?

@Joyca2 ,

Oui, c'est ce qu'il faut trouver.

Si besoin, je te rappelle la formule générale
$Zn=r×eiθZ^n=r\times e^{i\theta}$ d'où
$Z=r1n×ei(θn+2kπn)Z=r^\dfrac{1}{n}\times e^{i(\dfrac{\theta}{n}+\dfrac{2k\pi}{n})}$
pour $k$ entier compris entre 0 et $(n - 1)$

ici, $n = 3$

@mtschoon donc la on a fini vu qu'on a trouvé z ?

@Joyca2 , Quand tu auras fini les calculs (je ne vois pas ce que tu as trouvé pour $z$ .., je me demande même si tu as trouvé...), tu auras les 3 valeurs de z solutions de $z^3=2i$

L'ensemble de solutions de l'équation de départ sera composé de 6 valeurs : les 3 valeurs de $z$ correspondant à $z^3=-1$ et les 3 valeurs de $z$ correspondant à $z^3=2i$

@mtschoon le soucis ici ce qu'il y avait aucun problème a trouver les solutions de Z3 = -1 car nous pouvons elever facilement -1 au cubes qui va donner -1 ce qui n'est pas le cas avec Z au cubes = 2i, meme mis sous la forme exponentielles je ne vois pas comment déterminer k vu qu'apres remplacer nous avons trouver que z = à la racine cubique de 2eipi/2 ,je remarque ici que k n'est plus present donc je ne sais pas quoi faire. Pouvez-vous détailler votre raisonnement pour trouver les 3 solutions de Z*3= = 2i svp

@Joyca2 , OK mais faut que ce soit toi qui le trouve...

$Z3=2eiπ2Z^3=2e^{\dfrac{i\pi}{2}}$

Tu appliques la formule que je t'ai indiqué qui doit être dans ton cours et que tu dois savoir.

Tu appliques cette formule pour $n = 3$

$Z=213ei(π6+2kπ3)Z=2^{\dfrac{1}{3}}e^{i(\dfrac{\pi}{6}+\dfrac{2k\pi}{3})}$

Ensuite, tu trouves les 3 valeurs en remplaçant successivement $k$ par $0$ , puis $1$ puis $2$ .

@mtschoon Apres simplification, j'ai trouver que ZO = 2°1/3.e°i(pi/6)
Z1 = 2°1/3.e°i(5pi/6)
Z2 = 2°1/3.e°i(3pi/2)
Est-ce correct?

@Joyca2 , c'est bon. Bravo.

@mtschoon juste une petit question,sommes-nous obliger de le garder sous forme exponentielles car je souhaite le mettre sous forme decimale si possible.

@Joyca2 , c'est toi qui voit en fonction de la question et des habitudes de ton professeur.
Personnellement , dans ce type d'exercice, je préfère les formes exponentielles, car si l'on veut représenter les images dans le plan complexe, c'est rigoureux.

Les 6 solutions ayant des arguments remarquables, c'est possible, mais donne des valeurs exactes.

Exemple :
$213×eiπ6=213×(cosπ6+isinπ6)2^{\dfrac{1}{3}}\times e^{i\dfrac{\pi}{6}}=2^{\dfrac{1}{3}}\times (cos\dfrac{\pi}{6}+isin\dfrac{\pi}{6})$
$213×eiπ6=213×(32+i12)2^{\dfrac{1}{3}}\times e^{i\dfrac{\pi}{6}}=2^{\dfrac{1}{3}}\times (\dfrac{\sqrt 3}{2}+i\dfrac{1}{2})$
$213×eiπ6=(213)(32)+i(213)(12)2^{\dfrac{1}{3}}\times e^{i\dfrac{\pi}{6}}=(2^{\dfrac{1}{3}})(\dfrac{\sqrt 3}{2})+i(2^{\dfrac{1}{3}})(\dfrac{1}{2})$
Tu peux encore transformer les "2"
Au final :
$2(−23)2^{\dfrac{1}{3}}\times e^{i\dfrac{\pi}{6}}=2^{(-\dfrac{2}{3})}\sqrt 3+i\ 2^{(\dfrac{-2}{3})}$

Tu peux faire pareil pour les 5 autres solutions (si tu connais bien les angles remarquables) mais je ne vois pas l'interêt...

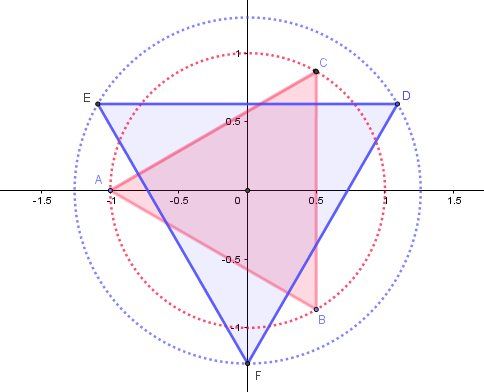
Tu peux faire une représentation graphique des 6 solutions de l'équation de départ.

Les points A,B,C sont les images des solutions de $z^3=-1$
Ils sont sur le cercle de centre O et de rayon 1
Ils sont les sommets du triangle équilatéral (rouge)

Les points D,E,F sont les images ds solutions de $z^3=2i$
Ils sont sur le cercle de centre O et de rayon $2132^\dfrac{1}{3}$
Ils sont les sommets du triangle équilatéral (bleu)