Calcul de la Limite d'une fonction
-
AAifasse dernière édition par
Bonjour je bloque sur un exercice c'est pour un dm aidez-moi svp
On me demande de calculer la limite suivante
lim [ 2x - E(x) ] / (x+1)
x→0
x<0
-
-
mtschoon dernière édition par mtschoon

@Aifasse, bonsoir,
@Noemi a dit dans Calcul de la Limite d'une fonction :
@Aifasse Bonjour,
Remplace xxx par 000.
Je ne suis pas d'accord avec cette proposition...désolée...
Losque x tend vers 0 par valeurs inférieures, x appartient à [-1,0[ donc E(x)=−1E(x)=-1E(x)=−1
La fonction s'écrit donc, dans ce cas,
2x−(−1)x+1=2x+1x+1\dfrac{2x-(-1)}{x+1}=\dfrac{2x+1}{x+1}x+12x−(−1)=x+12x+1la limite est simple à trouver. C'est 1.
-
@mtschoon Bonsoir,
C'est vrai que cette piste n'est pas rigoureuse, mais mon intention était de voir pourquoi Aifasse indiquait "Je bloque".
Avait-il noté le inférieur à 0 et partie entière ?
Dommage, je n'aurais certainement pas sa démarche car on lui a fourni la réponse.
-
mtschoon dernière édition par mtschoon

@Noemi , bonsoir,
Ta piste n'est pas bonne ( encore désolée ).
Regarde ce qu'a écrit @Aifasse
Il a très bien écrit sa question.
La proposition aurait été "non rigoureuse mais donnant une réponse exacte" s'il s'agissait de la limite à droite lorsque x tend vers 0.
Ainsi, x appartiendrait à [0,1[, donc E(x)=0=E(0).Ce n'est pas le cas ici.
Tout ceci n'est pas grave.
L'essentiel est que @Aifasse ait compris, et s'il n'a pas compris, il le demandera et on aura sa démarche.
-
AAifasse dernière édition par
@mtschoon donc si je comprends bien je peux partir directement en cherchant E(0)=-1 à gauche en fait je pensais que je devrais utiliser la formule pour déterminer la partie entière
n<(ou égal) E(x) < n+1 mais je ne savais pas comment la manipuler Merci beaucoup @mtschoon et @Noemi une fois de plus vous avez été d'une grande aide
-
mtschoon dernière édition par mtschoon

@Aifasse , ce que tu dis n'est pas correct.
Regarde ton cours sour la fonction partie entière.
Pour x∈[n,n+1[x\in[n,n+1[x∈[n,n+1[, E(x)=nE(x)=nE(x)=n ( avec n entier)
Donc :
Pour x∈[−1,0[ , E(x)=−1\boxed{x\in[-1,0[\ ,\ E(x)=-1}x∈[−1,0[ , E(x)=−1
Pour x∈[0,1[x\in[0,1[x∈[0,1[, E(x)=0E(x)=0E(x)=0Vu que tu cherches la limite, lorsque x tend vers 0 par valeurs inférieures à 0, tu es sur l'intervalle [-1,0[, donc E(x)=−1E(x)=-1E(x)=−1.
Tu rempaces donc E(x)E(x)E(x) par −1-1−1C'est la discontinuité de la fonction partie entière qui est en jeu ici.
-
AAifasse dernière édition par
@mtschoon désolé une erreur de ma part
n<(ou égale) x< n+1
comme x tend vers des valeurs inférieures à 0
Si je prend par exemple E(-0,8)= -1 ; E(-0,5)=-1
Donc E(0)=-1 lorsque x tend vers des valeurs inférieures à 0
-
mtschoon dernière édition par mtschoon

@Aifasse ,
Je pense que tu as compris mais ta formulation n'est pas bonne.
Pour x=0, E(x) ne peut pa prendre DEUX valeurs (-1 et 0) , sinon ce ne serait pas une fonction.E(−0,8)=−1;E(−0,5)=−1E(-0,8)= -1 ; E(-0,5)=-1E(−0,8)=−1;E(−0,5)=−1 c'est bon.
Tu peux même écrire E(−0.00000001)=−1E(-0.00000001)=-1E(−0.00000001)=−1 mais E(0)=−1E(0)=-1E(0)=−1 est FAUX car E(0)=0\boxed{E(0)=0}E(0)=0Lorsque x tend vers des valeurs inférieures à 0, tu ne peux pas remplacer x par 0 .
x prend des valeurs aussi voisines que l'on veut de 0 mais strictement inférieures à 0Tu peux (et dois) écrire limx→0,x<0 E(x)=−1\boxed{\displaystyle \lim_{x\to 0, x\lt 0}\ E(x)=-1}x→0,x<0lim E(x)=−1
La fonction partie entière n'est pas continue à gauche en 0
Il s'agit d'une fonction en escalier discontinue à gauche en 0 ( et pour toute valeur entière)
Pour x∈[−1,0[x\in[-1, 0[x∈[−1,0[ (intervalle fermé à -1 et ouvert à 0), on est sur la "marche" niveau -1
Pour x∈[0,1[x\in[0, 1[x∈[0,1[ (intervalle fermé à 0 et ouvert à 1), on est sur la "marche" niveau 0
En bref, il y a un saut à 0.
-
mtschoon dernière édition par mtschoon

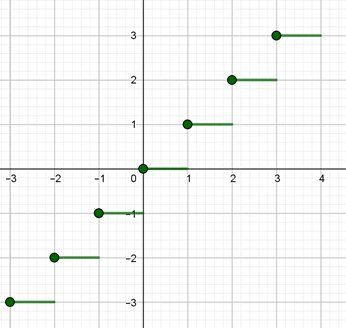
@Aifasse , pour plus de clarté, je te joins la représentation graphique de la fonction partie entière
Les segments et les points en font partie.Observe le point d'abscisse 0 et son voisinage.