Les fonctions reciproques

Bonjour,Pouvez-vous m'aider à resoudre cet exercice ?
Soit f(x)=√4−𝑥−√2+𝑥

Déterminer Domf, les racines de f, étudier le sens de variation de f.
Déterminer Imf.
La fonction f est-elle injective ? (justifie)
Effectue une ébauche du graphe de f(x) et de celui de sa réciproque.
Donne une expression algébrique de sa réciproque.
Que peux-tu dire de la tangente au graphe de la réciproque en son point d’ordonnée 4 ? (justifie)
Déterminer l’équation de la tangente au graphe de f(x) en son point d’abscisse 1. En déduire l’équation de la tangente au graphe de f-1 en son point d’abscisse 0.

@Joyca2 , bonjour,

Je te démarre l'exercice, seulement le début

$f(x)=4−x−2+xf(x)=\sqrt{4-x}-\sqrt{2+x}$

Conditions d'existence : $4−x≥04-x\ge 0$ et $2+x≥02+x\ge 0$
$4−x≥04-x\ge 0$ <=> $−x≥−4-x\ge -4$ <=> $x≤4x\le 4$
$2+x≥02+x\ge 0$ <=> $x≥−2x\ge -2$

L'ensemble de définition de f est donc $Df=[−2.4]\boxed{D_f=[-2.4]}$

Dans tout l'exercice , tu travailles avec $x∈[−2.4]x\in [-2.4]$

Pour les racines de f, tu cherches les solutions de $f (x) = 0$ c'est à dire $4−x=2+x\sqrt{4-x}=\sqrt{2+x}$

A toi de faire et donne tes réponses éventuellement.

@mtschoon j'ai deja trouver merci

@mtschoon je suis à det l'image

@Joyca2 a dit dans Les fonctions reciproques :

@mtschoon je suis à det l'image

@Joyca2 , avec le tableau de variations que tu as fait pour les variations de f , puisque tu dis que tu en être à $I m f$ , tu peux déduire $I m f$ directement.

$I m f$ est l'ensemble des valeurs de f(x), pour $x∈[−2,4]x\in[-2,4]$ .

Il te suffit de regarder ton tableau de variation.

.

@Joyca2 , pour que tu puisses vérifier ton tableau de variation, je t'en joins un :

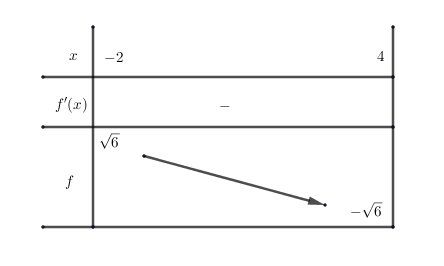
Ainsi, tu peux déduire que $Imf=[−6,6]Imf=[-\sqrt 6,\sqrt 6]$

@Joyca2 , bonjour,

Encore un exercice que tu postes et qui n'a pas abouti...

Un conseil : poste peut-être moins d'exercices mais travaille les jusqu'au bout pour qu'ils te soient utiles.

Je mets quelques pistes pour consultation éventuelle (seulement des pistes).

Vu l'étude des variations , f est définie dérivable donc continue et strictement croissante de $[- 2, 4]$ vers $[−6,6][-\sqrt 6 , \sqrt 6]$

Tout élément de l'ensemble d'arrivée $[−6,6][-\sqrt 6 , \sqrt 6]$ a un antécédent unique dans $[- 2, 4]$
f est donc une bijection de $[- 2, 4]$ vers $[−6,6][-\sqrt 6 , \sqrt 6]$ .
Elle est à forciori injective comme le demande l'énoncé écrit, mais l'important est quelle soit bijection pour pouvoir étudier sa bijection réciproque.

Sur le graphique joint, la représentation graphique de $f$ est en bleu;

la représentation graphique de $f^{-1}$ (réciproque de $f$ ) est en rouge.
En repère orthonormé, ces deux représentations graphiques sont symétriques par rapport à la droite d'équation $y = x$ en noir.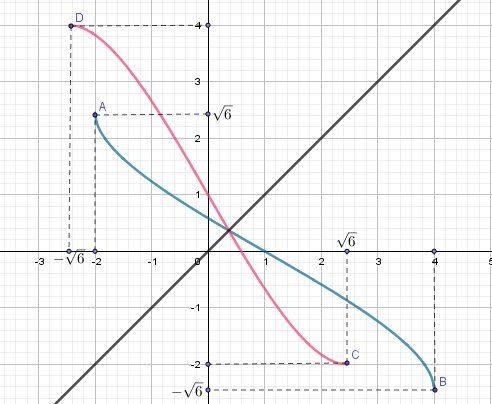

racinescarrées.pg.jpg

@Joyca2 a dit dans Les fonctions reciproques :

expression algébrique de sa réciproque

Piste de calcul de $f^{-1}(x)$

$y=f^{-1}(x)$ <=> $x = f (y)$

$x=4−y−2+yx=\sqrt{4-y}-\sqrt{2+y}$

Par élévétion au carré : $x2=6−2(4−y)(2+y)x^2=6-2\sqrt{(4-y)(2+y)}$

Par transposition : $2(4−y)(2+y)=6−x22\sqrt{(4-y)(2+y)}=6-x^2$

Après nouvelle élévation au carré, simplifications , division par 4, on arrive à :
$y2−2y+14x4−3x2+1=0y^2-2y+\dfrac{1}{4}x^4-3x^2+1=0$

Equation du second degré d'inconnue y.
Après calculs :
$Δ=−x4+12x2\Delta=-x^4+12x^2$

$y1=2−−x4+12x22y_1=\dfrac{2-\sqrt{-x^4+12x^2}}{2}$ et $y2=2+−x4+12x22y_2=\dfrac{2+\sqrt{-x^4+12x^2}}{2}$

Il faut choisir entre $y_1$ et $y_2$

Un test : il faut que, pour $x=6x=\sqrt 6$ , $y = - 2$
Après calcul, c'est $y_1$ qui convient.

Donc : $f−1(x)=2−−x4+12x22\boxed{f^{-1}(x)=\dfrac{2-\sqrt{-x^4+12x^2}}{2}}$

Pistes pour les tangentes demandées,

"Que peux-tu dire de la tangente au graphe de la réciproque en son point d’ordonnée 4 ?"

La tangente au graphe de $f^{-1}$ en son point d’ordonnée 4 (point D) est symétrique de la tangente au graphe de f d'abscisse 4 (point B)
Au point d'abscisse 4 du graphe de f, la fonction n'étant pas dérivable (taux tendant vers $+∞+\infty$ ) , la tangente est parallèle à l'axe des ordonnées.
Donc, par symétrie, La tangente au graphe de la réciproque $f^{-1}$ au point d’ordonnée 4 est parallèle à l'axe des abscisses.

Equation de la tangente au graphe de $f$ en son point d’abscisse 1 :
$y = f^{'} (1) (x - 1) + f (1)$ A calculer.

Equation de la tangente au graphe de $f^{-1}$ en son point d'ordonnée 1, c'est à dire d'abscisse 0 :
$y=(f^{-1})' (0)(x-0)+f^{-1}(0)$ A calculer
Remarque :
$(f−1)′(0)=1f′(1)(f^{-1})' (0)=\dfrac{1}{f'(1)}$

Bon travail éventuel ( il y a du travail dans cet exercice).