Ligne de niveau. chapitre vecteur

S'ils vous plait j'ai besoin d'aide pour démarré avec cet exercice, merci d'avance. Soit A et B deux points distincts. Construit l'ensemble des points M du plan tel que : $MA^2-MB^2 = 2AB^2$ .

Relation mise en Latex par la modération.

@Vassiriki-Doumbia je trouve que la somme des pondération est nul et les vecteurs MA et MB sont constant que fait après cela?

@Vassiriki-Doumbia Bonjour,

Choisis I milieu du segment $[A B]$ et utilise
$MA2−MB2=2MI→.BA→MA^2-MB^2=2\overrightarrow{MI}.\overrightarrow{BA}$

Bonjour,

Un petit plus, si besoin, @Vassiriki-Doumbia .

J'espère que tu as prouvé la formule qui t'est proposée, avec I mileu de [AB], si elle n'est pas dans ton cours.

$MA2−MB2=MA→2−MB→2MA^2-MB^2=\overrightarrow{MA}^2-\overrightarrow{MB}^2$
Avec la relation de Chasles :
$MA2−MB2=(MI→+IA→)2−(MI→+IB→)2MA^2-MB^2=(\overrightarrow{MI}+\overrightarrow{IA})^2-(\overrightarrow{MI}+\overrightarrow{IB})^2$
Après développement (identités remarquables) et simplifications, il reste :
$MA2−MB2=2MI→.IA→−2MI→.IB→MA^2-MB^2=2\overrightarrow{MI}.\overrightarrow{IA}-2\overrightarrow{MI}.\overrightarrow{IB}$
$MA2−MB2=2MI→.(IA→−IB→)MA^2-MB^2=2\overrightarrow{MI}.(\overrightarrow{IA}-\overrightarrow{IB})$
$MA2−MB2=2MI→.BA→MA^2-MB^2=2\overrightarrow{MI}.\overrightarrow{BA}$
En changeant le sens des deux vecteurs, on peut écrire :
$MA2−MB2=2IM→.AB→MA^2-MB^2=2\overrightarrow{IM}.\overrightarrow{AB}$

L'énoncé se traduit donc par :
$2IM→.AB→=2AB22\overrightarrow{IM}.\overrightarrow{AB}=2AB^2$ , c'est à dire
$IM→.AB→=AB2\boxed{\overrightarrow{IM}.\overrightarrow{AB}=AB^2}$ ,

Tu peux appeler H le projeté de M sur la droite (AB)
Avec le théorème de la projection, tu obtiens
$IH→.AB→=AB2\boxed{\overrightarrow{IH}.\overrightarrow{AB}=AB^2}$

Cette dernière égalité te permet de placer H sur la droite (AB).
Sachant où est H, vu que H est le projeté de M sur (AB) tu peux construire l'ensemble des points M.

Reposte si besoin.

Salut @mtschoon s'il vous plaît ces H le projeté de M sur la droite AB, ou bien ces M le projeté de M sur la droite AB. Merci d'avance

@Vassiriki-Doumbia .

H est le le projeté de M sur la droite (AB)

H est le pied de la perpendiculaire à la droite (AB), issue de M.

Si tu préfères :

M se projette (orthogonalement ) en H, sur la droite (AB)

Tu peux éventuellement regarder ici I )1 ) 3) cas de 2 vecteurs quelconques.
https://www.mathforu.com/premiere-s/produit-scalaire-et-applications-en-1ere-s/

Merci @mtschoon pour votre contribution

De rien @Vassiriki-Doumbia

J'ignore si tu as placé le point H au bon endroit.
Pour pouvoir vérifier , je te joins un schéma.
Bien sûr, l'ensemble des points M est la droite (D) passant par H et perpendiculaire à (AB).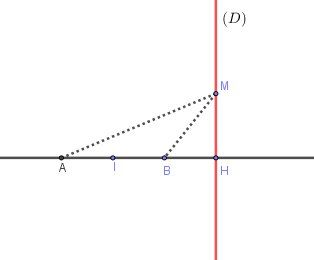

Reposte si besoin.