Ligne de niveau chapitre vecteur

[Vassiriki Doumbia]

On considère un triangle équilatéral ABC tel que:AB=AC=BC=1. soit A' le milieu du segment [AB]
Détermine l'ensemble des points M du plan tels que:2MA^2+MB^2+MC^2= 2. S'ils vous plaît aider moi

[Noemi]

@Vassiriki-Doumbia Bonjour (Marque de politesse ne pas oublier !!!)

Utilise la relation $M{A}^2+M{B}^2=2M{A}^{\prime 2}+\frac{A{B}^2}{2}$
On débute avec $M{A}^2=(\overrightarrow{M{A}^{\prime }}+\overrightarrow{A^{\prime }A}{)}^2=...$

Si tu n'as pas cette relation dans le cours, demande la démonstration (proche de ton exercice précédent) si tu ne parviens pas à la réaliser.

[mtschoon]

Bonjour,

Bizarre ...
Dans l'énoncé, j'aurais mis A' milieu de [BC]
???

[mtschoon]

@Vassiriki-Doumbia , je te donne quelques pistes , en supposant que A' est le milieu de [BC]

Il y a deux méthodes .

La méthode rapide est l'utilisation directe de l'expression $aM{A}^2+bM{B}^2+cM{C}^2$ en utilisant le barycentre G de $(A,a)(B,b)(C,c)$
Si tu as la formule dans ton cours, tu peux l'utiliser (mais ce n'est pas sûr que tu l'aies)

Sinon, tu utilises la méthode utilisant les points deux par deux.
Je te donne des pistes pour cette méthode un peu plus longue, mais bien adaptée à ton exercice.

Avec la formule que tu as vu dans ton exercice précédent:
$M{B}^2+M{C}^2=2M{A}^{\prime 2}+\frac{B{C}^2}{2}$
$M{B}^2+M{C}^2=2M{A}^{\prime 2}+\frac{1}{2}$

En remplaçant dans l'expression de l'énoncé :
$2M{A}^2+M{B}^2+M{C}^2=2$ <=> $2M{A}^2+2M{A}^{\prime 2}+\frac{1}{2}=2$
c'est à dire : $2M{A}^2+2M{A}^{\prime 2}=\frac{3}{2}$
c'est à dire : $M{A}^2+M{A}^{\prime 2}=\frac{3}{4}$

Soit G le milieu de [AA']
Avec la même propriété : $2M{G}^2+\frac{A{A}^{\prime 2}}{2}=\frac{3}{4}$

Tu continues en isolant $M{G}^2$ , en calculant $A{A}^{\prime 2}$
Tu obtiendras ainsi la valeur de $M{G}^2$, puis de $MG$ et tu pourras conclure sur l'ensemble des points M.

Reposte si tu a besoin d'aide ou si tu veux une vérification de tes réponses.

[Black-Jack]

Bonjour,

Alternative (probablement pas attendue, bien que très efficace ici) :

Choix d'un repère tel que :
A(0;0) , B(1;0) , C(1/2 , (V3)/2) (avec V pour racine carrée)
Et M(x;y)

On calcule facilement MA², MB² et MC² en fonction de x et y

Et en appliquant 2MA² + MB² + MC² = 2, on a l'équation du lieu des points M, qu'il est facile de mettre sous une forme connue et ...

---

[mtschoon]

Bonjour,

Effectivement,@Vassiriki-Doumbia travaille visiblement les propriétés du produit scalaire(+barycentres) et de ses applications géométriques ; pas de calculs analytiques en vue , j'imagine...
Je pense que ce n'est pas le but recherché.

[mtschoon]

@Vassiriki-Doumbia , bonsoir,

Pour que tu puisses vérifier tes résultats, je te mets un schéma.
L'ensemble des points M est le cercle (noir).
Mais, bien sûr, il faut le prouver.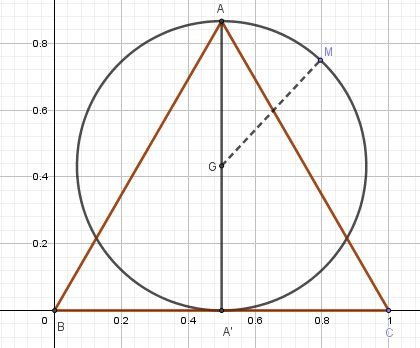

Bon travail.

Reposte si besoin.