Limites et continuité

Bonsoir car j’ai du mal à finir ma question j’ai déjà fait mon tableau de variation mais je sais pas comment faire là suite ,pouvez-vous m’aider s’il vous plaît.
-soit g une fonction définie sur IR par g(x)=x^3-3x-4,étudier le sens de variations de g sur IR.Démontrer que l’équation g(x)=0 admet une unique solution sur IR notée a donné une valeur approchée puis en déduire le signe de g(x) sur IR.

@ytbtenin-glamour Bonsoir,

Utilise le théorème des valeurs intermédiaires.

Bonjour,

@ytbtenin-glamour , je t'indique, pour vérification, le tableau de variation que tu as dû trouver.

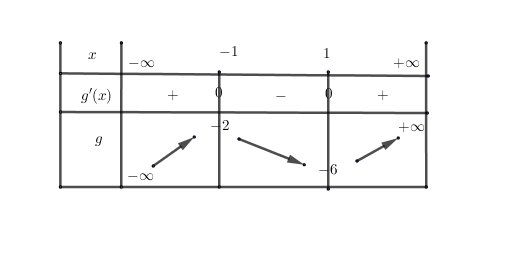
Conséquence :

Sur $]−∞,1]]-\infty,1]$ , $g(x)≤−2g(x)\le -2$ donc à forciori, $g(x)<0g(x)\lt 0$
L'équation g(x)=0 n'a pas de solution dans $]−∞,1]]-\infty,1]$

Sur $]1,+∞[]1,+\infty[$ , g est dérivable donc continue et strictement croissante de $]1,+∞[]1,+\infty[$ vers $+\infty[$

Comme te l'indique Noemi, applique le TVI sur $]1,+∞[]1,+\infty[$
$0∈]−6,+∞[0\in ]-6, +\infty[$
0 a un antécédent unique dans $]1,+∞[]1,+\infty[$
L'équation g(x)=0 a une solution unique a dans $]1,+∞[]1,+\infty[$

Conclusion générale : L'équation g(x)=0 a une solution unique a dans $R$

@ytbtenin-glamour , illustration graphique

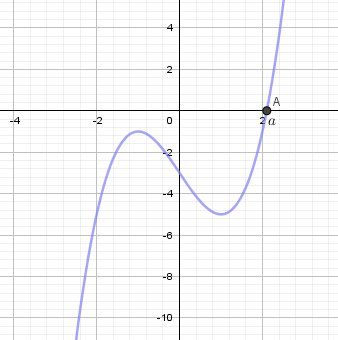
Pour une valeur approchée de $a$ , tu n'indiques pas la précision à donner...
Utilise ta calculette . Tu dois trouver $a≈2.2a\approx 2.2$

Tu déduis le signe de $g (x)$ sur $R$ .
Pour $x<ax\lt a$ : $g (x)$ ...................................(tu compètes)
Pour $x = a$ : $g (x) = 0$
Pour $x>ax\gt a$ : $g (x)$ ...................................(tu complètes)

Bon travail.
Reposte si besoin.

@mtschoon merci beaucoup

De rien @ytbtenin-glamour .
J'espère que tout est clair pour toi.