logarithme népérien ln

bonsoir
g(x)=1+ $x^2$ - 2 $x^2$ lnx
il me demande de montrer gue l'équation g(x)=0 admet dans]0,+00[ une unique solution \alpha,
comment je peut répondre a cette question s'il vous plais

@baraa-skhairi, bonsoir,

@baraa-skhairi a dit dans logarithme népérien ln :

g(x)=1+ $x^2$ - 2 $x^2$ lnx
montrer gue l'équation g(x)=0 admet dans]0,+00[ une unique solution \alpha,
comment je peux répondre a cette question

Piste,

Tu étudies les variations de $g$ sur $]0,+∞[]0,+\infty[$

Pour cela, tu calcules $g^{'} (x)$
Sauf erreur, tu dois trouver $g^{'} (x) = - 4 x l n (x)$

$x>0x\gt 0$ donc $g^{'} (x)$ est du signe de $- l n (x)$

Tu fais le tableau de variations de g sur $]0,+∞[]0,+\infty[$

Sur $] 0, 1]$ , $g$ croissante de 1 à 2
Pour $x = 1$ , $g (x) = 2$
Sur $[1,+∞[[1,+\infty[$ , g décroissante de 2 à $−∞-\infty$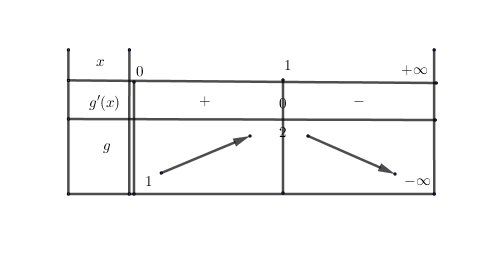

Conséquence :

Sur $]−∞,1]]-\infty,1]$ , $g(x)>0g(x)\gt 0$ donc pas de solution à l'équation $g (x) = 0$

Sur $]1,+∞[]1,+\infty[$ , g continue ( car dérivable) est strictement décroissante . tu appliques le TVI.

$0∈]−∞,2[0\in ]-\infty,2[$ donc 0 a un antécédent unique $α\alpha$ dans $]1,+∞[]1,+\infty[$
$g (x) = 0$ a donc une solution unique $α\alpha$ dans $]1,+∞[]1,+\infty[$

BILAN : $α\alpha$ est l'unique solution de $g (x) = 0$ dans $]0,+∞[]0,+\infty[$

Tu peux trouver une valeur approchée de $α\alpha$ avec ta calculette.
$α≈1.9\alpha\approx 1.9$

@mtschoon oui je vois merci beaucoup

comment je peux calculer la limite de g lorsque x tend vers +00

@baraa-skhairi ,

Pour x tendant vers $+∞+\infty$

Tu peux mettre $x^2$ en facteur

$g(x)=x^2[1-2ln(x)]+1$

Ensuite,

$x^2$ tend vers $+∞+\infty$
$[1 - l n (x)]$ tend vers $−∞-\infty$
donc le produit $x^2[1-ln(x)]$ tend vers - $∞\infty$

Tu termines et tu trouves $−∞-\infty$

@mtschoon
oui oui
j'ai une petite confusion ,j'ai pensé que l'infini multiplié par l'infini est une forme indéterminée
merci bien a vos effort c'etait bien clair

De rien @baraa-skhairi , c'est bien si maintenant c'est clair pour toi.

@baraa-skhairi ,

Illustration graphique

Bon DM !

@baraa-skhairi , bonjour,

Lorsque tu as une question complémentaire, reste sur ton topic initial pour la poser (et n'ouvre pas une autre discussion car le multipostage n'est pas autorisé.)

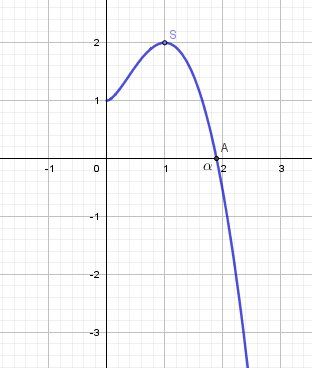
Conséquence sur le signe de $g (x)$

Avec l'étude faite et en regardant la représentation graphique correspondant à cette étude, le signe de g(x) est immédiat :

$g(x)>0g(x)\gt 0$ pour $0<x<α0\lt x\lt \alpha$
$g (x) = 0$ pour $x=αx=\alpha$
$g(x)<0g(x)\lt 0$ pour $x>αx\gt \alpha$