Fonction racine carrée, asymptotes, graphique
-
*__mnl__elm__* dernière édition par Noemi
Bonjour j'ai besoin d'aide pour un devoir sur les fonctions
Voici l'énoncé : on considère la fonction f(x)= x+ Racine carré de x² -2x+ a où a désigne un paramètre Supérieur ou égal à 1.(A) déterminer le domf
(B) déterminez les éventuelles assymptotes
(C) faites un graphique
Merci à ceux qui prendront le temps de me répondre
-
@__mnl__elm__ Bonjour,
La fonction est-elle ? f(x)=x+x2−2x+af(x)= x+\sqrt{x^2-2x+a}f(x)=x+x2−2x+a
Si oui, pour la question (A) résous l'inéquation : x2−2x+a≥0x^2-2x+a \geq 0x2−2x+a≥0
que tu peux écrire sous la forme : (x−1)2+a−1≥0(x-1)^2+a-1 \geq0(x−1)2+a−1≥0
-
*__mnl__elm__* dernière édition par
@Noemi Je vois et donc pour l'exercice B pour calculer mes assymptotes je peux partir du même calcul ?
-
Calcule les limites en +∞+\infty+∞ et −∞-\infty−∞.
Cherche l'asymptote oblique.
-
mtschoon dernière édition par mtschoon

Bonjour,
Tu ne dis pas ce que tu as trouvé comme ensemble de définition.
Avec la piste de @Noemi , j'espère que tu as trouvé Df=RD_f=RDf=RJe suis surprise que l'étude des variations de f ne soit pas demandée...
Tu aurais dû trouver dérivée positive donc fonction croissante.Quelques pistes pour les limites.
Lorsque x tend vers −∞-\infty−∞, tu as une forme indéterminée du type "∞−∞\infty-\infty∞−∞"
Pour lever l'indétermination, pense à utiliser la quantité conjuguée.
f(x)=(x+x2−2x+a)(x−x2−2x+a)x−x2−2x+af(x)=\dfrac{(x+\sqrt{x^2-2x+a})(x-\sqrt{x^2-2x+a})}{x-\sqrt{x^2-2x+a}}f(x)=x−x2−2x+a(x+x2−2x+a)(x−x2−2x+a)f(x)=x2−(x2−2x+a)x−x2−2x+a=2x−ax−x2−2x+af(x)=\dfrac{x^2-(x^2-2x+a)}{x-\sqrt{x^2-2x+a}}=\dfrac{2x-a}{x-\sqrt{x^2-2x+a}}f(x)=x−x2−2x+ax2−(x2−2x+a)=x−x2−2x+a2x−a
f(x)=2x−ax−x2(1−2/x+a/x2)f(x)=\dfrac{2x-a}{x-\sqrt{x^2(1-2/x+a/x^2)}}f(x)=x−x2(1−2/x+a/x2)2x−a
Tu sais que x2=∣x∣\sqrt{x^2}=|x|x2=∣x∣
Pour x<0x\lt 0x<0 , x2=−x\sqrt{x^2}=-xx2=−x
Donc f(x)=2x−ax+x1−2/x+a/x2f(x)=\dfrac{2x-a}{x+x\sqrt{1-2/x+a/x^2}}f(x)=x+x1−2/x+a/x22x−a
Tu mets xxx en facteur au numérateur et au dénominateur.
Tu simplifies par xxx
Tu en déduis la limite :
limx→−∞f(x)=1\boxed{\displaystyle\lim_{x\to -\infty}f(x)=1}x→−∞limf(x)=1
La droite d'équation y=1y=1y=1 est donc asymptote à la courbe en −∞-\infty−∞
-
mtschoon dernière édition par mtschoon

En +∞\infty∞, il n'y a pas d'indétermination
Tu dois trouver :
limx→+∞f(x)=+∞\boxed{\displaystyle \lim_{x\to +\infty}f(x)=+\infty}x→+∞limf(x)=+∞Il peut donc y avoir une asymptote oblique de la forme y=ax+by=ax+by=ax+b.
Pour trouver aaa , tu cherches la limite de f(x)x\dfrac{f(x)}{x}xf(x) :
Tu dois trouver, sauf erreur :
limx→+∞f(x)x=2\displaystyle \lim_{x\to +\infty}\dfrac{f(x)}{x}=2x→+∞limxf(x)=2 donc a=2\boxed{a=2}a=2Ensuite, pour trouver bbb, tu cherches la limite de f(x)−axf(x)-axf(x)−ax
Tu dois trouver, sauf erreur :
limx→+∞[f(x)−2x]=−1\displaystyle \lim_{x\to +\infty}[f(x)-2x]=-1x→+∞lim[f(x)−2x]=−1 don b=−1\boxed{b=-1}b=−1En +∞+\infty+∞, la courbe a une asymptote oblique l'équation : y=2x−1\boxed{y=2x-1}y=2x−1
Tous les calculs sont à faire en +∞+\infty+∞ .
Je t'ai seulement donné piste/résultats.Resposte si besoin.
-
*__mnl__elm__* dernière édition par
@mtschoon merci beaucoup de votre aide je suis tombée sur le même résultat. Bonne soirée à vous
-
mtschoon dernière édition par

De rien @__mnl__elm__ ,
C'est parfait si tu as tout démontré.
Bonne soirée à toi.
-
mtschoon dernière édition par

Bonjour,
Illustration graphique
Les deux asymptotes sont en rouge
Les courbes d'équation y=x+x2−2x+ay=x+\sqrt{x^2-2x+a}y=x+x2−2x+a sont représentées pour a=2,a=3,a=4,a=5a=2, a=3,a=4,a=5a=2,a=3,a=4,a=5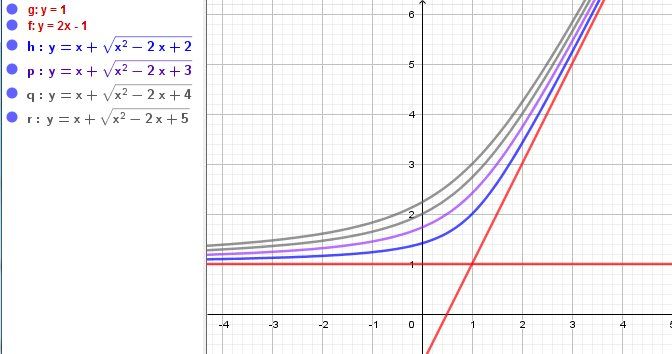
-
*__mnl__elm__* dernière édition par
@mtschoon merci énormément, je rencontrais quelques difficultés pour le graphique. Bonne fin de journée à vous
-
mtschoon dernière édition par mtschoon

@__mnl__elm__ , de rien et bonne soirée à toi.
-
mtschoon dernière édition par mtschoon

@__mnl__elm__ , bonjour,
Evidemment a∈]1,+∞[a\in ]1,+\infty[a∈]1,+∞[
aaa peut prendre une infinité de valeurs et à chaque valeur de aaa correspond une courbe.
Tu peux te contenter que prendre une valeur pour aaa (strictement supérieure à 1) ou quelques valeurs pour améliorer l'illustration.A+