Probabilité Mathématiques complémentaires

Bonjour, j'ai besoin d'aide pour cet exercice de probabilités niveau Terminale maths complémentaires.

Un détecteur de faux billet est constitué d'une lampe qui s'allume en bleu lorsque le détecteur considère que le billet est vrai et en rouge lorsqu'il considère que le billet est faux.

On note F l'évènement « Le billet testé est faux » et B l'évènement « La lumière bleue s'allume ».

Le détecteur n'étant pas infaillible, il se peut qu'il commette des erreurs de détection. On estime que la probabilité qu'un billet soit vrai sachant que la lumière bleue s'est allumée est égale à 95 % et que la probabilité qu'un billet soit faux sachant que la lumière rouge s'est allumée est égale à 95 %.

Reproduire et compléter les pointillées de l'arbre de probabilité.
Exprimer P(F) en fonction de P(B).
On note p la probabilité qu'un billet soit

a. Montrer que:

P(B)= (0.95 - p)/0,9

b. En déduire que 0,05 ≤ p ≤ 0,95.

Montrer que

P sachant F (B) = (0.95-p) / 18p

Interpréter ce résultat dans le contexte de l'exercice.

On note f la fonction définie pour tout réel x appartenant à l'intervalle (0,05 ; 0,95] par:

f(x) = (0.95 - x) / 18x

a. Dresser le tableau de variation de la fonction f sur l'intervalle [0,05; 0,95)

b. Tracer à la calculatrice la courbe représentative de la fonction f.

c. Résoudre graphiquement l'inéquation f(x)≥0,95 sur l'intervalle [0,05; 0,95].

d. Retrouver le résultat par une résolution algébrique.

La qualité du détecteur se mesure au fait que la lumière rouge s'allume chaque fois que le billet est faux. Compte tenu de contraintes techniques, cette situation idéale n'est pas possible.

Déterminer les valeurs de p pour que la probabilité que la lumière rouge s'allume quand le billet est faux soit au moins de 95 %.

Ces valeurs sont-elles réalistes ?

Pour l'arbre il est assez simple je l'ai fait mais je bloque à la deuxième question

Merci d'avance

@maybessa , bonjour,

Pistes pour démarrer,

Je te mets l'arbre pour clarifier l'exercice

Notations :
B : bleu
R : rouge (c'est à dire "non bleu")
F : faux
V : vrai (c'est à dire "non faux")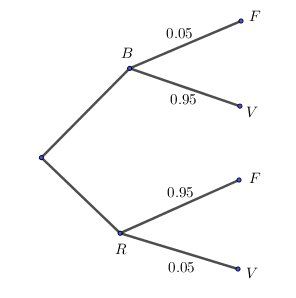

Il faut exprimer p(F) en fonction de p(B)

Utilise l'arbre (il est fait pour ça)
$p(F)=p(B)×0.05+p(R)×0.95p(F)=p(B)\times 0.05+p(R)\times 0.95$
$p(F)=p(B)×0.05+(1−p(B))×0.95p(F)=p(B)\times 0.05+(1-p(B))\times 0.95$
Tu développes et tu simplifies et tu dosi obtenir
$p(F)=−0.9p(B)+0.95\boxed{p(F)=-0.9p(B)+0.95}$

Tu transposes :
$0.9 p (B) = 0.95 - p (F)$
En divisant par $0.9$ , tu obtiens
$p(B)=0.95−p(F)0.9p(B)=\dfrac{0.95-p(F)}{0.9}$

Ce que tu appelles p, ce n'est pas clair dans ton énoncé, mais je suppose que p(F)=p

D'où $p(B)=0.95−p0.9\boxed{p(B)=\dfrac{0.95-p}{0.9}}$

Essaie de poursuivre.

@mtschoon salut monsieur svp je suis très faible en probabilité et statistiques pouvez-vous m'aider à finir cet exercice pour que je puisse m'en servir pour en faire d'autres je vous en prie

@quatiane-TSamo , bonjour.

Une remarque sans importance : ce n'est pas "Monsieur" mais "Madame".

@quatiane-TSamo , ce n'est pas toi qui a posé cet exercice fort long (6 grosses questions) c'est @maybessa.
Ici, on aide à faire les exercices mais on ne donne pas les solutions toutes faites.

(il existe des sites qui, en donnant l'énoncé, envoient toute la solution rédigée, peut-être par mail, je ne sais pas exactement...)

Il est préférable d'attendre que @maybessa dise où elle en est dans son exercice.
Après, on verra...

Bonjour,

Visiblement, @maybessa n'a pas demandé d'explications complémentaires.

Quelques pistes (réduites, car les calculs ne sont pas explicités) pour consultation éventuelle.

Pour prouver que $0.05≤p≤0.950.05\le p\le 0.95$

$p(B)=0.95−p0.9p(B)=\dfrac{0.95-p}{0.9}$

Toute probabilité est comprise entre 0 et 1 donc :
$0≤0.95−p0.9≤10\le \dfrac{0.95-p}{0.9}\le 1$

$0.95−p≥00.95-p\ge 0$ <=> $p≤0.95\boxed{p\le 0.95}$

$0.95−p≤09×10.95-p\le 09\times 1$ <=> $p≥0.95−0.9p\ge 0.95-0.9$ <=> $p≥0.05\boxed{p\ge 0.05}$

Question 4)

$\cap F)=p_B(F)\times p(B)=0.05\times \dfrac{0.95-p}{0.9}$

$pF(B)=p(B∩F)p(F)=0.05×0.95−p0.9pp_F(B)=\dfrac{p(B\cap F)}{p(F)}=0.05\times \dfrac{0.95-p}{0.9p}$

Après transformations , on trouve :
$pF(B)=0.95−p18p\boxed{p_F(B)=\dfrac{0.95-p}{18p}}$

Question 5)

$f(x)=0.95−x18xf(x)=\dfrac{0.95-x}{18x}$ pour $0.05≤x≤0.950.05\le x\le 0.95$
( $x$ représente $p$ c'est à dire $p (F)$ )

f est définie, dérivable.
Après calcul, $f′(x)<0f'(x)\lt 0$ donc f décroissante.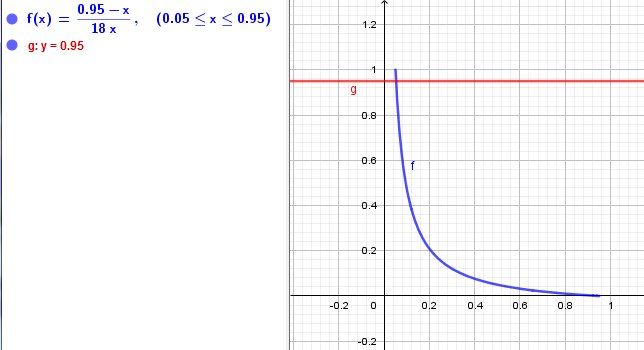

Graphiquement, les valeurs de x telles que $f(x)≥0.95f(x)\ge 0.95$ sont les abscisses des points de la courbe situés au-dessus de la droite (rouge) d'équation $y = 0.95$ ( à lire..., mais pas très lisible...)

Algébriquement, on résout : $0.95−x18x≥0.95\dfrac{0.95-x}{18x}\ge 0.95$

Après calculs ( multiplication par $18 x$ , transposition, division pour isoler $x$ ), sauf erreur, on trouve approxomativement $x≤0.052486x\le 0.052486$

Question 6)

$pF(R)≥0.95p_F(R)\ge 0.95$ <=> $1−pF(B)≥0.951-p_F(B)\ge 0.95$ <=> $pF(B)≤0.05p_F(B)\le 0.05$
On doit donc résoudre $0.95−p18p≤0.05\dfrac{0.95-p}{18p}\le 0.05$
Sauf erreur, on trouve $p≥0.5p\ge 0.5$

Comme l'indique l'énoncé, ces valeurs ne sont pas réalistes...

Bons calculs éventuels.

@mtschoon
Bonsoir désolé de revenir que maintenant j'ai avance dans l'exercice donc pour la 3.b j'ai répondu

On a p(b)> 0 et 0,9>0 donc 0,95-p>0
Et donc p<0,95
On a également p(b)< 1 donc
0,95-p<0,9
Donc -p<-0,05
Donc 0,05<p<0,95

@maybessa Bonjour,

Oui, cela correspond aux éléments de réponse fournis précédemment.

@Noemi

J'essaie de faire la question de 4 depuis un moment mais je n'arrive pas à faire les transformations pour obtenir 18p je n'obtiens que des 0,045 ou d'autres j'ai essayé de faire des produits en croix mais je n'y arrive pas, il faut factoriser? Par quoi sinon?
Merci d'avance

@maybessa

Le $18$ du dénominateur correspond à $0,90,05=18\dfrac{0,9}{0,05}=18$ .

Ou écrire $0, 9$ sous la forme $\times 18$ .

@Noemi
D'accord merci beaucoup j'avais fait tout les calculs sauf ça merciii

@maybessa mais pourquoi on divise le dénominateur par le numérateur ?

@maybessa

$0,050,9=10,90,05=118\dfrac{0,05}{0,9}=\dfrac{1}{\dfrac{0,9}{0,05}}=\dfrac{1}{18}$
ou tu écris :
$0,050,9=0,050,05×18=118\dfrac{0,05}{0,9}=\dfrac{0,05}{0,05\times18}=\dfrac{1}{18}$

@maybessa ,

Noemi t'a fait le calcul.

On divise $0.05$ du numérateur par $0.9$ du dénominateur pour obtenir la forme de l'expression demandée par l'énoncé : remplacer $0.050.9\dfrac{0.05}{0.9}$ par $118\dfrac{1}{18}$

@mtschoon

D'accord merci j'ai compris
Je viens de faire la question 5 et j'ai vérifié avec vos réponses j'ai fait le tableau de variation qui est sur l'intervalle 0,05;0,95 et j'ai résolu a la calculatrice pour trouver leur images donc c'est décroissant et pour f'(x) c'est de signe - non?

Pour l'inequation j'ai fait ça :

0,95-x/18x > 0,95
0,95-x>17,1x
0,95>18,1x
0,95/18,1>x
X< 0,052486

@maybessa

Concernant la question 6 je n'ai pas compris ce que je devais faire merci

@maybessa ,

Ton calcul. est bon.

f est bien décroissante par $f′(x)<0f'(x)\lt 0$ (si tu as bien calculé $f^{'} (x)$ .

@maybessa , pour la question 6), relis l'énoncé :

"Déterminer les valeurs de p pour que la probabilité que la lumière rouge s'allume quand le billet est faux soit au moins de 95 %"

Il faut donc que tu résolves $pF(R)≥0.95p_F(R)\ge 0.95$

En passant par l'évènement contraire $p_F(R)=1-p_F(B)$ , tu dois donc trouver $p$ tel que :
$1−pF(B)≥0.951-p_F(B)\ge 0.95$