Équation différentielle
-
KKodak dernière édition par
Bonjour, s'il vous plaît pouvez vous m'aider avec ça
(e^x + e^(2x))y' + (2e^x+ e^(2x))y+1=0
J'ai essayé mais je suis pas sûre de mon résultat.
Merci!!
-
@Kodak Bonjour,
Indique ton résultat et nous le validerons ou nous te donnerons des pistes de résolution.
-
BBlack-Jack dernière édition par
Bonjour,
Une manière parmi d'autres ...
(e^x + e^(2x))y' + (2e^x+ e^(2x))y+1=0
Poser X = e^x (et donc X est toujours différent de 0)
dX = e^x dx
dx = dX/Xy' = dy/dx = X.dy/dX
L'éuation devient : (X + X²)X.dy/dX + (2X+X²).y + 1 = 0
dy/dX + y * (2X+X²)/((X + X²)X) + 1/((X + X²)X) = 0 puisque X est différent de 0)
dy/dX + y * (2+X)/(X + X²) = - 1/((X + X²)X)Solutions de dy/dx + y * (2+X)/(X + X²) = 0
dy/dx = -y * (2+X)/(X + X²)
dy/y = - dx * (2+X)/(X + X²)(2+X)/(X + X²) = (2+X)/(X(X+1)) = A/X + B/(X+1) et par manière habituelle, on montre que A = -2 et B = 1
dy/y = (-2/X + 1/(X+1))dX
ln|ky| = ln|(X+1)/X²|
y = C*(X+1)/X²Solution particulière de dy/dX + y * (2X+X²)/((X + X²)X) + 1/((X + X²)X) = 0
Par variation de la constante: y = f*(X+1)/X² (avec f une fonction de X)dy/dX = f'(X+1)/X² - f(2+X)/X³
L'équation devient : f'(X+1)/X² - f(2+X)/X³ + f*(X+1)/X² * (2X+X²)/((X + X²)X) = -1/((X + X²)X)
Après simplification ... :
f'(X+1)/X² = -1/((X + X²)X)
f'(X+1)/X² = -1/((1 + X)X²)
f' = -1/(1+X)²
Et donc f = 1/(1+X)
Une solution particulière de dy/dX + y * (2X+X²)/((X + X²)X) + 1/((X + X²)X) = 0 est donc y = 1/(1+X) * (X+1)/X²
soit y = 1/X²Solutions générales de (X + X²)X.dy/dX + (2X+X²).y + 1 = 0 :
y = 1/X² + C*(X+1)/X²
y = (1 + C*(X+1))/X²Et avec X = e^x, les solutions générales de (e^x + e^(2x))y' + (2e^x+ e^(2x))y+1=0 sont :
y = (1 + C*(1 + e^x)) / e^(2x) ou si on préfère :
y=e−2x∗(1+C∗(1+ex))y = e^{-2x} * (1 + C*(1 + e^x))y=e−2x∗(1+C∗(1+ex))
Avec C = constante
Rien relu.
On peut aussi se passer du changement de variables initial (X = e^x) et procéder presque de la même manière ...
Tu peux essayer à titre d'exercice.
-
BBlack-Jack dernière édition par Black-Jack
Oups, pas vu le message de Noemi avant d'envoyer le mien.
De toutes manières, valider un résultat est facile, il suffit de le dériver et remettre y' et y dans l'équation de départ pour voir si c'est OK.
-
KKodak dernière édition par
@Noemi
Bonjour
J ai trouver,xe^-2x+e^-x+a(e^-x(1+e^x)
J ai essayé par variations de la constante
-
KKodak dernière édition par
@Black-Jack
Bonjour, merci, je vais réessayer
-
La résolution de l'équation homogène associée donne pour résultat sauf erreur de calcul :
y=ae−x(1+e−x)y= ae^{-x}(1+e^{-x})y=ae−x(1+e−x)
Une solution particulière de l'équation y=−e−xy = -e^{-x}y=−e−x
La solution générale :
y=e−x(a+ae−x−1)y= e^{-x}(a+ae^{-x}-1)y=e−x(a+ae−x−1)
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Je pense que si les solutions générales sont : y = e^-x * (a + a*e^-x - 1), il y a un soucis ...
y' = ...
Et cela donne au final (sauf erreur de la part) : (e^x + e^(2x))y' + (2e^x+ e^(2x))y+1 = - a (et pas 0)
Si j'entre l'équation différentielle de départ dans mon singe ... il me donne les solutions (sans la démarche) et voila ce que cela donne :
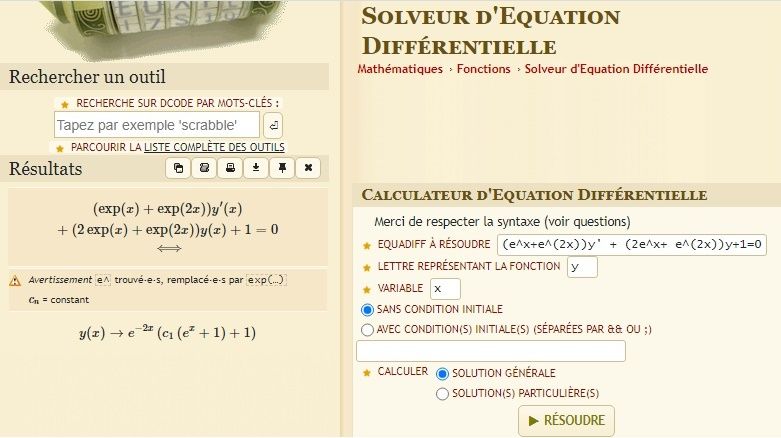
Solutions finales conformes à ma réponse.
-
KKodak dernière édition par
@Noemi
Merci beaucoup, je vais réessayer
-
BBlack-Jack dernière édition par
Rebonjour,
Je ne suis pas d'accord avec la solution particulière donnée par Noemi.
Une solution particulière correcte est y = e^(-2x)
Et cette fois, en l'associant aux solutions de l'équation homogène y = a*e^-x * (1 + e^-x)
On trouve les solutions générales : y = e^(-2x) + a*e^-x * (1 + e^-x)
Qui peuvent s'écrire aussi : y = e^(-2x) * (1 + a (1 + e^x))
Et on retrouve les solutions que j'ai proposées dans ma réponse initiale.
-
mtschoon dernière édition par mtschoon

Bonjour,
Seulement une réflexion relative aux résultas relatifs à cette équation différentielle.
Il y a deux résultats qui semblent différents mais qui, malgré les apparences, sont totalement identiques.ANALYSE de ces résultats.
Première réponse y1=e−2x[1+C(1+ex)]y_1=e^{-2x}[1+C(1+e^x)]y1=e−2x[1+C(1+ex)]
avec CCC constante réelle.En développant : y1=e−2x(Cex+C+1)\boxed{y_1=e^{-2x}(Ce^x+C+1)}y1=e−2x(Cex+C+1)
Deuxième réponse y2=ae−2x(ex+1)+f(x)y_2= ae^{-2x}(e^x+1)+f(x)y2=ae−2x(ex+1)+f(x)
avec aaa constante réelle.
f(x)f(x)f(x) étant une solution particulière quelconque de l'équation générale .En développant : y2=e−2x(aex+a)+f(x)\boxed{y_2=e^{-2x}(ae^x+a)+f(x)}y2=e−2x(aex+a)+f(x)
Le théorème utilisé est valable sans exception quelle que que soit la solution particulière utilisée.
Il n'y a pas de solution particulière meilleure qu'une autre.
Suivant la valeur de f(x)f(x)f(x) utilisée, c'est la constante qui change.
-
mtschoon dernière édition par mtschoon

Deux solutions particulières f(x)f(x)f(x) ont été trouvées.
1er cas : f(x)=e−2xf(x)=e^{-2x}f(x)=e−2x
d'où y2=e2x(aex+a+1)\boxed{y_2= e^{2x}(ae^x+a+1)}y2=e2x(aex+a+1)
Dans ce cas, les constantes CCC et aaa sont les mêmes et bien sûr y1=y2y_1=y_2y1=y22ème cas : y=−e−xy=-e^{-x}y=−e−x
d'où y2=e−2x(aex+a)−e−xy_2=e^{-2x}(ae^x+a)-e^{-x}y2=e−2x(aex+a)−e−xe−xe^{-x}e−x peut s'écrire e−2xexe^{-2x}e^{x}e−2xex , d'où:
y2=e−2x(aex+a)−e−2xexy_2=e^{-2x}(ae^x+a)-e^{-2x}e^xy2=e−2x(aex+a)−e−2xex
y2=e−2x(aex+a−ex)y_2=e^{-2x}(ae^x+a-e^x)y2=e−2x(aex+a−ex)
y2=e−2x[ex(a−1)+a]\boxed{y_2=e^{-2x}[e^x(a-1)+a]}y2=e−2x[ex(a−1)+a]Soit C=a−1C=a-1C=a−1, c'est à dire a=C+1a=C+1a=C+1
y2=e−2x(Cex+C+1]\boxed{y_2=e^{-2x}(Ce^x+C+1]}y2=e−2x(Cex+C+1]Bien sûr, y1=y2y_1=y_2y1=y2
CQFD.
Bonne journée.

-
BBlack-Jack dernière édition par
@mtschoon a dit dans Équation différentielle :
Deux solutions particulières f(x)f(x)f(x) ont été trouvées.
1er cas : f(x)=e−2xf(x)=e^{-2x}f(x)=e−2x
d'où y2=e2x(aex+a+1)\boxed{y_2= e^{2x}(ae^x+a+1)}y2=e2x(aex+a+1)
Dans ce cas, les constantes CCC et aaa sont les mêmes et bien sûr y1=y2y_1=y_2y1=y22ème cas : y=−e−xy=-e^{-x}y=−e−x
d'où y2=e−2x(aex+a)−e−xy_2=e^{-2x}(ae^x+a)-e^{-x}y2=e−2x(aex+a)−e−xe−xe^{-x}e−x peut s'écrire e−2xexe^{-2x}e^{x}e−2xex , d'où:
y2=e−2x(aex+a)−e−2xexy_2=e^{-2x}(ae^x+a)-e^{-2x}e^xy2=e−2x(aex+a)−e−2xex
y2=e−2x(aex+a−ex)y_2=e^{-2x}(ae^x+a-e^x)y2=e−2x(aex+a−ex)
y2=e−2x[ex(a−1)+a]\boxed{y_2=e^{-2x}[e^x(a-1)+a]}y2=e−2x[ex(a−1)+a]Soit C=a−1C=a-1C=a−1, c'est à dire a=C+1a=C+1a=C+1
y2=e−2x(Cex+C+1]\boxed{y_2=e^{-2x}(Ce^x+C+1]}y2=e−2x(Cex+C+1]Bien sûr, y1=y2y_1=y_2y1=y2
CQFD.
Bonne journée.

Bonjour,
Oui, erreur de calcul dans vérification ...
y = e^-x * (a + a*e^-x - 1)
y' = -e^-x * (a + ae^-x - 1) + e^-x * (-a * e^-x)
y' = -e^-x * (a + 2ae^-x - 1)Et remis dans : (e^x + e^(2x))y' + (2e^x+ e^(2x))y + 1=0 -->
-
(e^x + e^(2x)) * e^-x * (a + 2ae^-x - 1) + (2e^x+ e^(2x)) * e^-x * (a + ae^-x - 1) + 1 = 0
-
(1 + e^(x)) * (a + 2ae^-x - 1) + (2+ e^x) * (a + ae^-x - 1) + 1 = 0
-
a - 2ae^-x + 1 - a.e^x - 2a + e^x + 2a + 2ae^-x - 2 + 1 + a.e^x + a - e^x = 0
0 = 0
-
-
mtschoon dernière édition par mtschoon

@Black-Jack a dit dans Équation différentielle :
Bonjour,
Oui, erreur de calcul dans vérification ...
y = e^-x * (a + a*e^-x - 1)
y' = -e^-x * (a + ae^-x - 1) + e^-x * (-a * e^-x)
y' = -e^-x * (a + 2ae^-x - 1)Et remis dans : (e^x + e^(2x))y' + (2e^x+ e^(2x))y + 1=0 -->
-
(e^x + e^(2x)) * e^-x * (a + 2ae^-x - 1) + (2e^x+ e^(2x)) * e^-x * (a + ae^-x - 1) + 1 = 0
-
(1 + e^(x)) * (a + 2ae^-x - 1) + (2+ e^x) * (a + ae^-x - 1) + 1 = 0
-
a - 2ae^-x + 1 - a.e^x - 2a + e^x + 2a + 2ae^-x - 2 + 1 + a.e^x + a - e^x = 0
0 = 0
Re-bonjour,
Oui @Black-Jack , tu as bien fait de revoir ton erreur dans ta vérification , car cela créait une contradiction.
Maintenant tout est OK.
C'est parfait.
-
-
mtschoon dernière édition par mtschoon

Bonjour,
@Kodak a effacé son énoncé après plusieurs interventions ! ! !
Comme indiqué à plusieurs endroits dans les interventions, la question est :
Résoudre l'équation différentielle
(ex+e2x)y′+(2ex+e2x)y+1=0\boxed{(e^x+e^{2x})y'+(2e^x+e^{2x})y+1=0}(ex+e2x)y′+(2ex+e2x)y+1=0EDIT: l'énoncé a été restauré.