Distance minimale entre deux droites

Bonsoir je bute sur un dm de maths portant sur la géométrie dans l'espace et je suis totalement perdu... J'aimerai bien avoir de l'aide s'il vous plait

On considère les deux droites (d) et (d') suivantes

d : x=3+t
y=-4-3t
z=1+t

d' : x=-5-t
y=6+t
z=-3-t

1.a. Démontrer que les droites (d) et (d') ne sont pas coplanaires.

b. Démontrer que le vecteur w (1;0;-1) est orthogonal aux vecteurs directeurs des droites (d) et (d').

c. Justifier que le plan P contenant la droite (d) et le vecteur w admet pour équation cartésienne :

3x + 2y + 3z-4 = 0.

d. Démontrer que le plan Pet la droite (d') sont sécants en un point H' dont on précisera les coordonnées.

e. On note Alpha la droite passant par H' et de vecteur directeur w. Démontrer que la droite Alpha est perpendiculaire aux deux droites (d) et (d'), et déterminer les coordonnées du point H, intersection des droites (d) et Alpha.

On souhaite démontrer que, pour tout point M appartenant à (d) et tout point M' appartenant à (d'), on a l'inégalité MM' > HH'.

a. Montrer que le vecteur MM' peut s'écrire comme la somme de HH et d'un vecteur orthogonal à HH'.

b. En déduire que ||MM||² plus grand ou égal à ||HH||² et conclure.

Déterminer alors la distance minimale entre deux points des droites (d) et (d').

@suhn1 , bonjour,

Quelques pistes pour démarrer,

(d) : ${x=3+ty=−4−3tz=1+t\begin{cases} x=3+t\cr y=-4-3t\cr z=1+t \end{cases}$
(d) passe par le point $A (3, - 4, 1)$ et a pour vecteur directeur $U→(1,−3,1)\overrightarrow{U}(1,-3,1)$

(d’) : ${x=−5−t’y=6+t’z=−3−t’\begin{cases} x=-5-t’\cr y=6+t’ \cr z=-3-t’ \end{cases}$
(d’) passe par le point $B (- 5, 6, - 3)$ et a pour vecteur directeur $V→(−1,1,−1)\overrightarrow{V}(-1,1,-1)$

Remarque : j’ai changé le nom du paramètre de (d’) car si les paramètres des deux droites s’appellent pareil, cela peut occasionner des erreurs.

@suhn1 ,
Pour démontrer que (d) et (d') ne sont pas coplanaires, tu peux démontrer qu'elles sont ni parallèles ni concourantes.

Pour démontrer qu'elles ne sont pas parallèles, tu peux prouver que leurs vecteurs directeurs ne sont pas colinéaires.

Il y a plusieurs façons; tout dépend de ton cours.

Tu peux prouver qu'un déterminant de leurs coordonnées est non nul.

Tu peux prouver qu'il n'existe pas de réel k tel que : $U→=kV→\overrightarrow{U}=k\overrightarrow{V}$

Pour cela , soit :
${1=k(−1)−3=k(1)1=k(−1)\begin{cases}1=k(-1)\cr -3=k(1) \cr 1=k(-1)\end{cases}$
Ce système est impossible car $k$ ne peut pas prendre à la fois les valeurs $- 1$ et $- 3$

Pour démontrer qu'elles ne sont pas concourantes, tu résous le système :
${3+t=−5−t′−4−3t=6+t′1+t=−3−t′\begin{cases} 3+t=-5-t'\cr -4-3t=6+t'\cr 1+t=-3-t'\end{cases}$
Avec deux de ces équations, tu calcules t et t'.
En reportant dans l'équation restante, tu trouves une impossibilité.

Conclusion : (d) et (d') ne sont pas coplanaires.

Essaie de poursuivre et donne tes réponses pour vérification si tu le souhaites.

Bonjour,

Un schéma sans repère orthonormé de l'espace (donc sans tenir compte des coordonnées des points), seulement pour pouvoir suivre les questions de l'exercice.

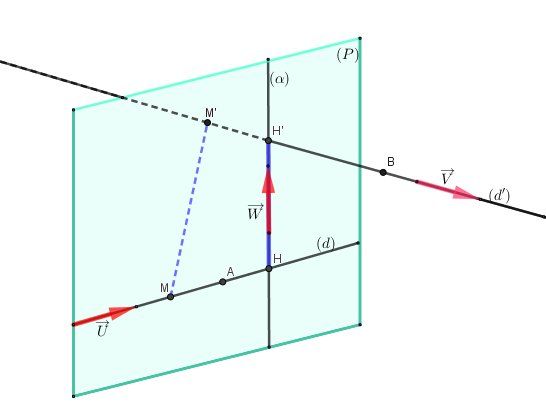
Une remarque : quelques faute de frappe dans l'écriture de la question 2 de @suhn1

Il faut lire :
"a. Montrer que le vecteur $MM′→\overrightarrow{MM'}$ peut s'écrire comme la somme de $HH′→\overrightarrow{HH'}$ et d'un vecteur orthogonal à $HH′→\overrightarrow{HH'}$ .

b. En déduire que || $MM′→\overrightarrow{MM'}$ ||² est plus grand ou égal à || $HH′→\overrightarrow{HH'}$ ||² et conclure"

Bonjour,

@suhn1 , tu n'a donné aucune réponse relative à l'aide donné pour le début de l'exercice, ni à la suite que tu as faite...
Ou bien tu as abandonné ou bien tu as terminé seul ...

Quelques indications (seulement des pistes) pour consultation éventuelle.

1)b) Calcul de 2 produits scalaires
$W→.U→=1(1)+0(−3)+(−1)(1)=0\overrightarrow{W}.\overrightarrow{U}=1(1)+0(-3)+(-1)(1)=0$
De même $W→.V→=0\overrightarrow{W}.\overrightarrow{V}=0$

1)c) La méthode la plus simple, vu l'équation de (P) qu'il faut trouver, est de prouver que le vecteur $T→(3,2,3)\overrightarrow{T} (3,2,3)$ est normal à (P)
$T→.W→=3(1)+2(0)+3(−1)=0\overrightarrow{T}.\overrightarrow{W}=3(1)+2(0)+3(-1)=0$
$T→.U→=3(1)+2(−3)+3(1)=0\overrightarrow{T}.\overrightarrow{U}=3(1)+2(-3)+3(1)=0$

Donc, $T→\overrightarrow{T}$ est bien vecteur normal à (P)
Une équation de (P) est de la forme $3 x + 2 y + 3 z + d = 0$
$A∈(P)A\in (P)$ : $3 (3) + 2 (- 4) + 3 (1) + d = 0$
après calcul : $d = - 4$
D'où équation de (P) : $3 x + 2 y + 3 z - 4 = 0$

1)d) On doit résoudre le système :
${3x+2y+3z−4=0x=−5−t′y=6+t′z=−3−t′\begin{cases} 3x+2y+3z-4=0 \cr x=-5-t'\cr y=6+t'\cr z=-3-t' \end{cases}$
Par substitution, on remplace x,y,z par leurs expressions en fonction de t' dans la première équation ce qui permet d'avoir la valeur de t' puis celles de x,y,z.
Sauf erreur, on trouve $H^{'} (- 1, 2, 1)$

1)e) $W→.U→=0\overrightarrow{W}.\overrightarrow{U}=0$ et $W→.V→=0\overrightarrow{W}.\overrightarrow{V}=0$ (déjà fait)
$(α)(\alpha)$ passe par H' et a pour vecteur directeur $W→\overrightarrow{W}$

d'où, représentation paramétrique de $(α)(\alpha)$ :
${x=−1+t′′y=2+t′′z=1+t′′\begin{cases}x=-1+t''\cr y=2+t''\cr z=1+t''\end{cases}$

En résolvant le système composé des des représentations graphiques de(d) et de $(α)(\alpha)$ , on obtient, sauf erreur $(H - 1, 2, - 1)$

2)a) $MM′→=MH→+HH′→+H′M′→\overrightarrow{MM'}=\overrightarrow{MH}+\overrightarrow{HH'}+\overrightarrow{H'M'}$

En regroupant :
$MM′→=HH′→+(MH→+H′M′→)\overrightarrow{MM'}=\overrightarrow{HH'}+(\overrightarrow{MH}+\overrightarrow{H'M'})$

D'après la question précédente, $MH→\overrightarrow{MH}$ et $M′H′→\overrightarrow{M'H'}$ sont orthogonaux à $W→\overrightarrow{W}$ donc le vecteur $(MH→+H′M′→)(\overrightarrow{MH}+\overrightarrow{H'M'})$ est orthognal à $W→\overrightarrow{W}$ donc à $HH′→\overrightarrow{HH'}$

2)b) $(MM′→)2=[HH′→+(MH→+H′M′→)]2(\overrightarrow{MM'})^2=[\overrightarrow{HH'}+(\overrightarrow{MH}+\overrightarrow{H'M'})]^2$

Après développemen( identité remarquable) et simplification par annulation d'un produit scalaire nul, il reste ;
$(MM′→)2=(HH′→)2+(MH→+H′M′→)2(\overrightarrow{MM'})^2=(\overrightarrow{HH'})^2+(\overrightarrow{MH}+\overrightarrow{H'M'})^2$
donc : $(MM′→)2≥(HH′→)2(\overrightarrow{MM'})^2\ge (\overrightarrow{HH'})^2$
donc $MM′≥HH′\boxed{MM'\ge HH'}$

CONCLUSION : la distance minimale entre deux points des droites (d) et (d') est $HH′\boxed {HH'}$

$HH′=(xH′−xH)2+(yH′−yH))2+(zH′−zH)2HH'=\sqrt{(x_H'-x_H)^2+(y_H'-y_H))2+(z_H'-z_H)^2}$

Sauf erreur $HH′=22HH'=2\sqrt 2$

Bonne lecteur et bons calculs éventuels.

Remarque : évidemment, avec le produit vectoriel, ce serait plus rapide, mais ce n'est pas au programme de Terminale actuellement.