Triangle tangent sous hyperbole

Bonjour nous avons besoin d'aide pour cette question s'il vous plait, voici l'énoncé. Merci d'avance !!
Soit H la branche d'hyperbole y = 1/x avec x >0. On note M le point de H d'abscisse m.
-La perpendiculaire à l'axe des abscisses passant par M coupe celui ci en H.
-La perpendiculaire à l'axe des ordonnées passant par M coupe celui ci en K.
-On note D la parallèle à la droite (HK) passant par M.
-La droite D coupe les axes des coordonnées en N et P (voir figure).
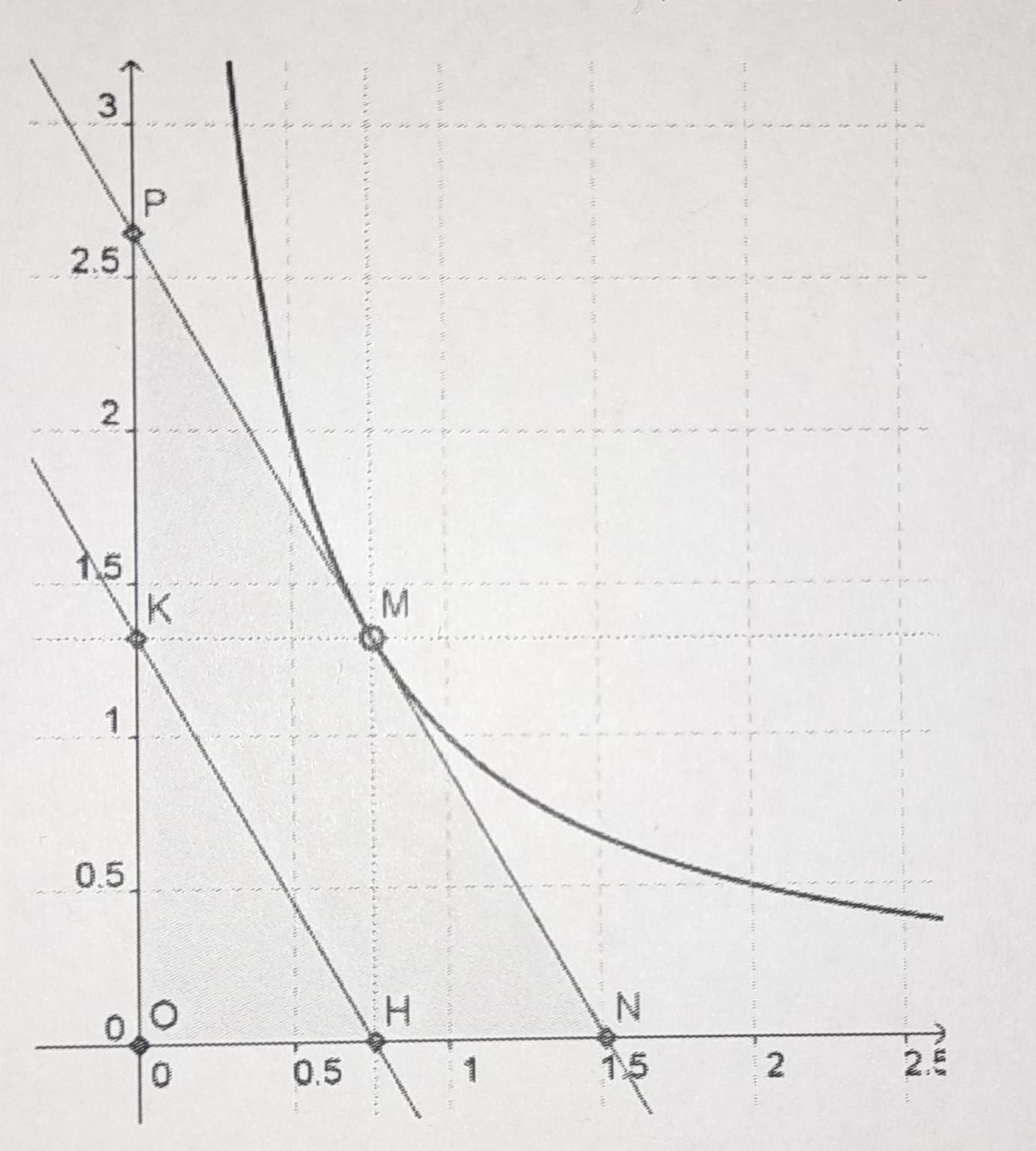
hyperbole .jpeg

Déterminer l'équation de la droite (HK). En déduire l'équation de D.
Montrer que la droite D est tangente à la courbe H.
Déterminer l'aire A(m) du triangle PON tangent en M à l'hyperbole.
Quelle est la valeur de m qui maximise cette aire ?

Merci

Bonjour/bonsoir @beox ,

Je regarde ton énoncé et je reste perplexe sur ta dernière question...sauf si j'ai mal lu les données( ?) à la question 3) tu dois trouver une aire ayant une valeur constante, alors il n'y a pas de valeur de m qui la maximise...
bizarre...vérifie l'énoncé.

Piste pour démarrer,

$m>0m\gt 0$
Equation de la droite (HK)
De la forme $y = a x + b$
$a=yK−yHxK−xH=1m−00−m=−1m2a=\dfrac{y_K-y_H}{x_K-x_H}=\dfrac{\dfrac{1}{m}-0}{0-m}=-\dfrac{1}{m^2}$

donc $y=−1m2x+by=-\dfrac{1}{m^2}x+b$

En utilisant, par exempele K : $1m=−1m2(0)+b\dfrac{1}{m}=-\dfrac{1}{m^2}(0)+b$
donc $b=1mb=\dfrac{1}{m}$

L'équation de (HK) est donc $y=−1m2x+1my=-\dfrac{1}{m^2}x+\dfrac{1}{m}$

(D) est parallèle à (HK) donc même coefficient directeur.
(D) a pour équation $y=−1m2x+By=-\dfrac{1}{m^2}x+B$

En utilisant le point M, tu dois trouver B , d'où l'équation de la droite (D)

Essaie de poursuivre.
Donne tes résultats pour vérification si tu le souhaites.

merci beaucoup je reste aussi bloquée face aux questions 3 et 4 je ne comprend pas pourquoi il y a m qui maximise pour l'aire (l'énoncé est correct) merci d'avance !!

pour la question 3 j'ai trouvé 1,875

@beox ,

Si tu en est à la question 3), c'est que tu as trouvé l'équation de (D) et que tu as démontré que (D) est tangente à (C)

Pour trouver l'aire du triangle PON tu utilises la formule usuelle :
$aire(PON)=OP×ON2aire(PON)=\dfrac{OP \times ON}{2}$

Vu que tu as l'équation de (D),
avec x=0, tu trouves OP
avec y=0, tu trouves ON

Tu peux donner ta réponse pour vérifcation si tu le souhaites.

Nos réponses se sont croisées...

@beox a dit dans Triangle tangent sous hyperbole :

pour la question 3 j'ai trouvé 1,875

Si tu parles de l'aire PON, ce n'est pas bon.
Donne éventuellement l'équation de (D) car tu as peut-être fait une erreur.

je n'ai pas trouvé l'équation malgré vos indications car dans votre premier message pour trouver a je n'ai pas compris comment vous avez fait

@mtschoon je pense oui avoir fait une erreur

@beox , il faut être rigoureux !

Tu dis :
@beox a dit dans Triangle tangent sous hyperbole :
je reste aussi bloquée face aux questions 3 et 4

Cela sous-entend que tu as fait les questions 1) et 2)...

Je reprends la question 1)
H a pour coodonnées $(m, 0)$
K a pour coordonnées $(0,1m)(0,\dfrac{1}{m})$

équation de (HK) : y=ax+b

Il y a plusieurs façons de faire.

Une façon :
Tu peux remplacer x et y par les coordonnées de H , puis par les coordonnées de K
Tu obtiens ainsi un système de deux équations à 2 inconnues a et b que tu résous.

Une autre façon un peu plus rapide que je t'ai indiqué.

Si tu connais : a est le coefficient directeur de la droite (HK) , que l'on obtient par : $abscissesa=\dfrac{différence\ des \ ordonnées}{différence\ des\ abscisses}$
c'est cela que j'ai utilisé.
ayant a , tu utilises les coordonnées de H ou de K pour trouver b.

Fais avec la méthode dont tu as l'habitude.
Tu trouveras pareil.

j'ai utilisé la deuxieme facon mais j'ai obtenu un résultat illogique contenant des k au cubes ce qui me semble etre mauvais donc je n'ai pas pu trouve la suite

@beox , avec la 2ème façon, j'espère que tu as trouvé

$a=−1m2a=-\dfrac{1}{m^2}$

$y=−1m2x+by=-\dfrac{1}{m^2}x+b$

En utilisant K, tu remplaces x par 0 et y par $1m\dfrac{1}{m}$

Cela donne :

$1m=−1m2×0+b\dfrac{1}{m}=-\dfrac{1}{m^2}\times 0 +b$

Lorsqu'on multiplie un nombre par 0 le résulta vaut 0, donc $−1m2×0-\dfrac{1}{m^2}\times 0$ vaut 0

Il reste : $1m=b\dfrac{1}{m}=b$

L'équation de (D) est donc : $y=−1m2x+1m\boxed{y=-\dfrac{1}{m^2}x+\dfrac{1}{m}}$

Remarque : au lieu d'utiliser les coordonnées de K, tu peux utiliser les coordonnées de H et tu trouveras la même valeur pour b.

revois cela et essaie de poursuivre.

ah ouuii mercccii ! j'avais pas compris a quoi correspondait le m mais maintenant c'est bon! je passe au 2

nous avons compris et reussi comment trouver l'équation mais n'avons pas compris comment en deduire que d est parallele

la suite de l'exercice est aussi compliquée

@beox

Tu as écrit, dans l'énoncé "On note D la parallèle à la droite (HK) passant par M"

Donc par hypothèse, (D)//(HK).

Comme déjà indiqué, vu que ces droites sont parallèles, le coefficient directeur de (D) est le même que le coefficient directeur de (HK) , c'est à dire $−1m2-\dfrac{1}{m^2}$

L'équation de (D) est de la forme $y=−1m2x+By=-\dfrac{1}{m^2}x+B$
(D) passe par $(m,\dfrac{1}{m})$
En remplaçant x et y respectivement par $m$ et $1m\dfrac{1}{m}$ , tu trouveras la valeur de B d'où l'équation de la droite (D)

Pour que tu puisse vérifier, je t'indique ce que tu dois trouver après calcul, pour (D) :
$y=−1m2x+2m\boxed{y=-\dfrac{1}{m^2}x+\dfrac{2}{m}}$

D'accord merci grace à cela j'ai 1/m au carré
cependant les questions suivantes je ne trouves pas comment les réaliser

@beox , si tu as maintenant trouvé l'équation de (D), il faut, d'après ton énoncé, démontrer que (D) est tangente à la courbe.

Il faut donc que tu prouves que (D) "touche" la courbe en un seul point (qui sera M)

Pour cela tu as les deux équations :
$y=1xy=\dfrac{1}{x}$ et $y=−1m2x+2my=-\dfrac{1}{m^2}x+\dfrac{2}{m}$

Tu cherches l'intersection, en résolvant le système
${y=1xy=−1m2x+2m\begin{cases}y=\dfrac{1}{x}\cr y=-\dfrac{1}{m^2}x+\dfrac{2}{m}\end{cases}$

l'égalité des $y$ te donne : $1x=−1m2x+2m\dfrac{1}{x}=-\dfrac{1}{m^2}x+\dfrac{2}{m}$

Tu transposes : $1m2x−2m+1x=0\dfrac{1}{m^2}x-\dfrac{2}{m}+\dfrac{1}{x}=0$

Tu peux multiplier par $m^2$ ( $m2>0)m^2\gt 0)$ ce qui donne $-2m+\dfrac{m^2}{x}=0$

Tu peux multiplier par $x$ ( $x>0x\gt 0$ ) ce qui donne $x^2 -2mx+m^2=0$

Tu dois reconnaitre un carré parfait(identité remarquable) ce qui te permettra de trouver la valeur de x cherchée.

merci beaucoup,
j'ai trouvé x=m mais je n'arrive pas à savoir si le m est tangent a la courbe H

@beox ,

Oui c'est bien $x = m$ donc $1x=1m\dfrac{1}{x}=\dfrac{1}{m}$

Tu viens ainsi de prouver que la droite (D) "touche" la courbe en un seul point : le point M
La droite (D) ne peut pas être sécante à la courbe, sinon il y aurait 2 points d'intersection (M et un autre)
C'est ce qu'à voulu te faire faire l'énoncé pour prouver que (D) est tangente.

Remarque : si tu étais en Première, tu pourrais utiliser la dérivée, mais en Seconde, tu ne connais pas...

Passe à la question 3) maintenant (si ce n'est pas déjà fait).
Dans une réponse précédente (croyant que tu avais résolu les 2 premières questions), je t'ai donné des indications pour la faire..

Oui merci cependant je trouve OP = 2/m et ON = 0, cela me parait bizarre étant donné que cela donne une aire de 0

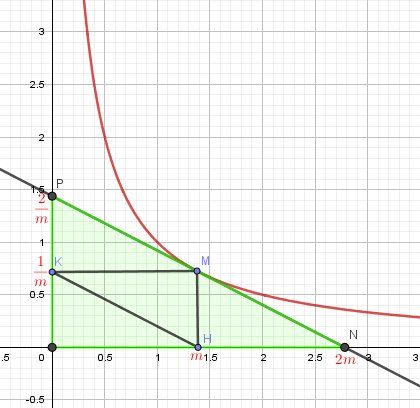
@beox , pour illustration , je te joins un schéma.
Dans le graphique donné avec ton énoncé, il n'y a qu'un exemple numérique .Visiblement, la valeur de $m$ choisie est $0.75$ .

Vu qu'il faut que tu fasses des calculs généraux avec $m$ quelconque strictement supérieur à 0, je te conseille un schéma où l'abscisse de M est $m$

Merci pour cette illustration, dois-je calculer KMH ? Je suppose que ma réponse de OP = 2/m et ON = 0 n'est donc pas correct ? la réponse peut être littérale ou forcément numérique ?? merci d'avance

@beox , c'est bon pour OP.

ON ne peut pas valoir 0

L'ordonnée de N est nulle $y = 0$

Tu dois résoudre $0=−1m2x+2m0=-\dfrac{1}{m^2}x+\dfrac{2}{m}$

Tu transposes : $1m2x=2m\dfrac{1}{m^2}x=\dfrac{2}{m}$

Tu divises par $1m2\dfrac{1}{m^2}$ ou tu multiplies par $m^2$ et tu dois trouver $x = 2 m$

Pour la 3), l'aire à calculer est l'aire PON

Pour la réponse relative à cette aire, le calcul est forcément littéral mais la réponse peut être un nombre fixé s'il y a des simplifications...

A toi de donner la valeur que tu trouves.

Je trouves A(m) = 2/m x 2m le tout divisé par 2
Ce qui nous donne A(m) = 2/m x m en simplifiant par deux puis 2/m x m/1 = 2
L'aire serait donc de 2

@beox , OUI !

Super ! Merci
Pour la question 4 je ne comprend pas comment on trouve la valeur de m qui maximise cette aire

@beox , effectivement....

C'est pour cela qu'en début de discussion je t'ai demandé si l'énoncé était exact, ce que tu m'as confirmé.

"Avec mauvais esprit" on peut dire que cette question est "stupide" ou que celui qui a fait les calculs et écrit l'énoncé "ne sait pas compter"...

"Sans mauvais esprit", on peut dire que cette question est "piégeuse"

Tu ne peux répondre que par la négation.

Vu que pour tout $m>0m\gt 0$ , l'aire $A (m)$ vaut 2 unités d'aire, elle est constante.

Il n'existe donc pas de valeur de $m$ qui maximise cette aire.

@mtschoon d'accord, donc je mets juste que ce n'est pas possible, comme réponse?
Que signifie qu'elle est constante?
Est ce l'ensemble 0?

@beox ,

"Constante" veut dire qu'elle ne varie pas.

Vu que quel que soit $m$ , l'aire du "Triangle tangent sous hyperbole" comme tu l'as écrit dans le titre vaut toujours 2 unités d'aire, cette aire est constante.

"l'ensemble 0" je ne sais pas de quoi tu parles...

D'accord merci donc si je comprend bien cette aire n'a pas de valeur qui maximise ou qui minimise m , elle est toujours à 2 unités d'aire ?

@beox , ta phrase n'est pas correcte mais je pense que tu as bien compris .

Il n'y a pas de valeur de $m$ qui maximise ou minimise cette aire.

@mtschoon je voulais dire l'ensemble vide le 0 barré

@beox , oui, tu peux dire que l'ensemble des valeurs de $m$ qui maximisent l'aire (ou la minimisent ) est l'ensemble vide.

@mtschoon D'accord merci beaucoup pour cette aide très précieuse !!!

De rien @beox .

Pour que tout soit clair pour toi, je te conseille de refaire seul la totalité de l'exercice.

Bon DM !

Merci c'est ce que je comptais faire maintenant que tout est clair, je vous tiendrais au courant de la fructuosité de la note obtenue

@beox , d'accord.
Bon dimanche