Equation complexe de degrés 4

Bonjour,
Cela fait un bout de temps que cherche la réponse a une équation donné lors d'un concours mais je ne trouve pas la méthode de résolution l'équation est z^4=1+i.
D'après la correction la solution est
plus ou moins racine 8ieme de 2 * e^(7ipi/16)
et plus ou moinss racine 8ieme de 2 * e^(-ipi/16)
Cela m aiderai beaucoup qu elle a été la méthode pour obtenir ce résultat

@nathan0202 Bonjour,

Quelle est l'écriture exponentielle de $1 + i$ ?
Puis tu prends la racine quatrième.

Bonjour,

@nathan0202 , tu cherches donc les racines 4ème de $1 + i$ .

Si dans ton cours tu as fait l'étude des racines nièmes d'un nombre complexe non nul , tu appliques directement le théorème avec $n = 4$

Je te joins une vidéo qui l'explique et qui l'applique à un exemple.

https://www.youtube.com/watch?v=Ztr0zbn-LHw

Bonjour,

Si ce qui te gène est de trouver des solutions différentes de l'énoncé ... tu peux être rassuré.

Le corrigé est faux.

Le corrigé donne les solutions de z^4 = 1 - i et pas de ce que l'énoncé annonce.

@nathan0202 , si tu n'a pas le théorème dans ton cours, tu peux faire tous les calculs
C'est plus long évidemment, mais c'est assez simple.

Je t'indique la démarche.

Tu mets $1 + i$ sous forme exponentielle : $1+i=2eiπ41+i=\sqrt 2 e^{i\dfrac{\pi}{4}}$

Soit $z=reiθz=re^{i\theta}$
$z^4=1+i$ <=> $(reiθ)4=2eiπ4(re^{i\theta})^4=\sqrt 2 e^{i\dfrac{\pi}{4}}$
c'est à dire ; $r4e4iθ=2eiπ4r^4e^{4i\theta}=\sqrt 2 e^{i\dfrac{\pi}{4}}$

Egalité des modules : $r4=2r^4=\sqrt 2$ <=> $r=(2)14r=(\sqrt 2)^{\dfrac{1}{4}}$
Tu peux l'écrire avec des exposants ou de radicaux (c'est pareil)

$r=(212)14=218r=\biggr (2^{\dfrac{1}{2}}\biggr)^{\dfrac{1}{4}}=2^{\dfrac{1}{8}}$
Tu peux aussi écrire $r=224=28r=\sqrt[4]{\sqrt[2] 2}=\sqrt[8] 2$

A la calculette $r≈1.0905r\approx 1.0905$

Egalité des arguments : $4θ=π4+2kπ4\theta=\dfrac{\pi}{4}+2k\pi$ avec $k∈Zk\in Z$

En divisant par 4 : $θ=π16+2kπ4\theta =\dfrac{\pi}{16}+\dfrac{2k\pi}{4}$ avec $k∈Zk\in Z$

Conclusion : $ei(π16+2kπ4)\boxed{z=\sqrt[8] 2 \ e^{i(\dfrac{\pi}{16}+\dfrac{2k\pi}{4})}}$

On obtient tous les arguments-solutions en donnant à $k$ quatre valeurs entières consécutives.
Par tradition, on prend $k = 0, 1, 2, 3$ mais on peut l'exprimer différemment.

Dans le plan complexe, les images des solutions forment un polygone régulier , ici un carré.

@nathan0202 ,
Je te mets la représentation graphique des solutions dans le plan complexe
:

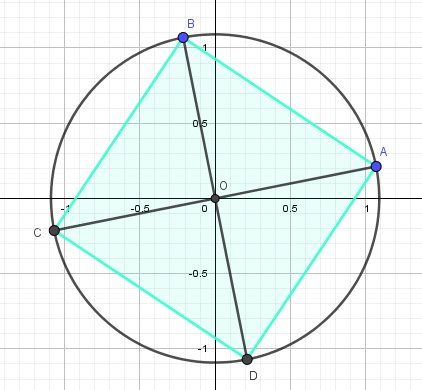Les points A,B,C D sont les images des solutions respectivement pour $k = 0, 1, 2, 3$ .

Tu as écrit

D'après la correction la solution est
plus ou moins racine 8ieme de 2 * e^(7ipi/16)
et plus ou moins racine 8ieme de 2 * e^(-ipi/16)

Je te fais la correspondance avec ta correction :

A et C (pour k=0 et k=2) ne correspondent pas à la seconde ligne de ta réponse
Il aurait fallu écrire "plus ou moins racine 8ieme de 2 * e^(pi/16)",

C et D ( pour k=1 et k=3) ne correspondent pas à la première ligne de ta réponse
Il aurait fallu écrire "plus ou moins racine 8ieme de 2 * e^(-7ipi/16)",

Ou bien tu as fait une faute en écrivant l'énoncé/ou réponses, ou bien il y a une faute dans ce qui t'est donné (regarde la proposition de @Black-Jack )

VERIFIE.

Bonjour,

Oui il aurait fallu écrire "plus ou moins racine 8ieme de 2 * e^(-7i.pi/16)"

Mais il aurait aussi fallu écrire "et plus ou moins racine 8ieme de 2 * e^(i.pi/16)"

Aucune des 4 solutions du corrigés ne correspond aux solutions de z^4 = 1 + i, elles correspondent toutes aux solutions de z^4 = 1 - i

Bonjour,

Tout à fait, Black Jack.

@nathan0202 vérifiera si c'est une faute de frappe de sa part ou si c'est une faute de son énoncé .

J'espère qu'avec la vidéo et les explications, il aura compris la méthode.

@mtschoon Oui désolé c'est de ma faute excuser moi l'énonce dit bien z^4=1-i

@mtschoon Merci beaucoup pour l'explication détailler.

De rien @nathan0202 ,

Si tu as bien compris la méthode, tu peux maintenant traiter le cas de $1 - i$
$e−iπ41-i=\sqrt 2\ e^{-i\dfrac{\pi}{4}}$
Tu dois trouver que les racines 4ème de (1-i) s'écrivent :
$ei(−π16+2kπ4)\boxed{z=\sqrt[8]2\ e^{i(\dfrac{-\pi}{16}+\dfrac{2k\pi}{4})}}$ pour $k∈Zk\in Z$

Tu peux bien sûr écrire : $ei(−π16+kπ2)\boxed{z=\sqrt[8]2\ e^{i(\dfrac{-\pi}{16}+\dfrac{k\pi}{2})}}$ pour $k∈Zk\in Z$

Ces racines ont pour images les points E,F,G,H du schéma ci dessous

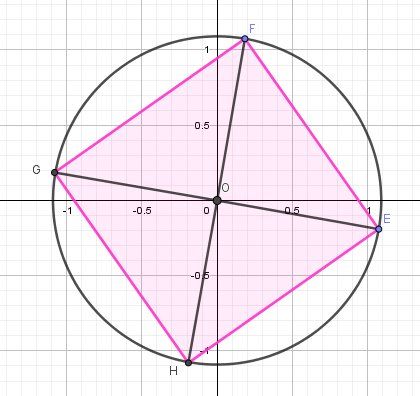
Bons calculs.