Devoir maison maths seconde
-
Lleab111 dernière édition par
Bonsoir, je vous écris car je rencontre des difficultés avec cet exercice de maths. Je bloque énormément dessus et j’espère recevoir de l’aide de votre part. Je dois le rentre demain
Merci d’avance et bonne soirée
-
@leab111 Bonsoir,
Le scan de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Ecris l'énoncé, indique tes éléments de réponse et la question qui te pose problème et tu obtiendras des pistes de résolution.
-
Hhadydu13 dernière édition par
@Noemi bonjour j’ai un problème de math pour demain et j’ai besoin d’aide.
Une association souhaite crée un drapeau de 8m sur 10m du type ci contre.
Mais par souci d’équilibre ,la commande stipule que le drapeau doit avoir une surface claire et une surface foncé égale.
Pour cela ,on considere Un rectangle ABCD tel que AB=8m et AD=10m.
M est un point variable sur le segment [AB].On considère le point J du segment [AD] et le point I tels que AMIJ soit un carré.
On note H le pointe d’intersection des droites (IJ) et (BC)et k le pointe d’intersection des droites (MI)et(CD).
1.Ou placer le point M pour que l’aire foncée soit égale à la surface claire?
2. Ou placer le point M pour que la surface foncée soit la plus petite possible? Que vaut alors cette aire?
-
mtschoon dernière édition par mtschoon

Bonjour,
Il y a deux demandeurs sur cet exercice ? ? ?
@hadydu13 , je regarde ton énoncé
Une association souhaite crée un drapeau de 8m sur 10m du type ci contre.
Mais par souci d’équilibre ,la commande stipule que le drapeau doit avoir une surface claire et une surface foncé égale.
Pour cela ,on considere Un rectangle ABCD tel que AB=8m et AD=10m.
M est un point variable sur le segment [AB].On considère le point J du segment [AD] et le point I tels que AMIJ soit un carré.
On note H le pointe d’intersection des droites (IJ) et (BC)et k le pointe d’intersection des droites (MI)et(CD).
1.Ou placer le point M pour que l’aire foncée soit égale à la surface claire?
2. Ou placer le point M pour que la surface foncée soit la plus petite possible? Que vaut alors cette aire?Les scans d'énoncés ne sont pas autorisés ici, mais, comme indiqué, les scans sont autorisés pour les schémas.
Tu aurais dû donner le schéma du drapeau , car on ne sait pas quelle est la partie claire et la partie foncée.
Je te joins le graphique du rectangle ABCD et les données indiquées.
Merci de préciser qu'elle est la partie claire et la partie foncée
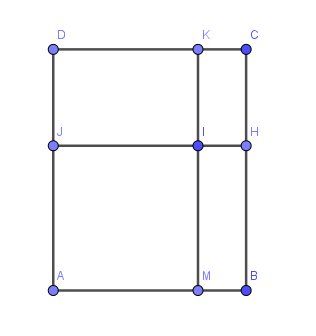
@hadydu13 a dit dans Devoir maison maths seconde :
@Noemi bonjour j’ai un problème de math pour demain et j’ai besoin d’aide.
-
Hhadydu13 dernière édition par
Ce message a été supprimé !
-
Hhadydu13 dernière édition par
@mtschoon le carré AMIJ et le rectangle CKIH sont foncés le reste et constituer de zone claire
-
BBlack-Jack dernière édition par
Bonjour,
Choisissons AM = x
MB = 8 - x
BH = x
HC = 10 - xTu peux alors calculer l'aire de (AMIJ) en fonction de x
et tu peux calculer l'aire de (CKIH) en fonction de xLa somme des 2 aires ci-dessus doit faire la moitié de l'aire totale, soit donc 1/2 * 10 * 8 = 40 (m²)
...
-
Hhadydu13 dernière édition par
@Black-Jack c’est la réponse à la questions 1?
-
mtschoon dernière édition par mtschoon

Re-bonjour,
@hadydu13 a dit dans Devoir maison maths seconde :
@Black-Jack c’est la réponse à la questions 1?
Je dirais qu'il s'agit des éléments nécessaires pour répondre à la question 1)
En m² :
aire(AMIJ)+aire(CHIH)=x2+(8−x)(10−x)aire(AMIJ)+aire(CHIH)=x^2+(8-x)(10-x)aire(AMIJ)+aire(CHIH)=x2+(8−x)(10−x)
Aire(ABCD)=80Aire(ABCD)=80Aire(ABCD)=80Vu que l'aire foncée doit être égale à l'aire claire, chacune doit valeur 40 (m²)
Il faut donc trouver xxx ( 0≤x≤8)0\le x\le 8)0≤x≤8) tel que :
x2+(8−x)(10−x)=40x^2+(8-x)(10-x)=40x2+(8−x)(10−x)=40
-
Hhadydu13 dernière édition par
@mtschoon et là questions 2
-
mtschoon dernière édition par mtschoon

J'espère que tu as terminé la question 1)
Piste pour la 2)
Soit f(x)f(x)f(x) l'aire de la zone foncée , toujours pour x compris entre 0 et 8
f(x)=aire(AMIJ)+aire(CKIH)f(x)=aire(AMIJ)+aire(CKIH)f(x)=aire(AMIJ)+aire(CKIH)
f(x)=x2+(8−x)(10−x)=2x2−18x+80f(x)=x^2+(8-x)(10-x)=2x^2-18x+80f(x)=x2+(8−x)(10−x)=2x2−18x+80
Tu étudies les variations de f pour x∈[0,8]x\in[0,8]x∈[0,8] pour trouver la valeur de xxx telle que f(x) soit minimale.
-
Hhadydu13 dernière édition par
@mtschoon je n’es pas reusi la 1 vous pouvez m’aider ?
-
mtschoon dernière édition par mtschoon

Pistes pour résoudre l'équation
x2+(8−x)(10−x)=40x^2+(8-x)(10-x)=40x2+(8−x)(10−x)=40Tu développes, tu transposes , tu simplifies et tu dois trouver:
2x2−18x+40=02x^2-18x+40=02x2−18x+40=0En divisant par 2 : x2−9x+20=0x^2-9x+20=0x2−9x+20=0
Vu que tu postes en Seconde, tu ne dois pas connaître les formules de résolution.
Tu dois passer par la forme cononique (identités remarquables):
(x−92)2−(92)2+20=0(x-\dfrac{9}{2})^2-(\dfrac{9}{2})^2+20=0(x−29)2−(29)2+20=0
Après calculs, tu dois trouver :
(x−92)2−(12)2=0(x-\dfrac{9}{2})^2-(\dfrac{1}{2}) ^2=0(x−29)2−(21)2=0Ensuite, tu factorises le membre de gauche avec l'identité a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b) à et tu termines.
-
Hhadydu13 dernière édition par
@mtschoon j’ai pas reusi la 2 aussi vous pouvez m’aider ?
-
mtschoon dernière édition par

Indique d'abord ta réponse à la 1), pour que les questions soient faire , à peu près, dans l'ordre.
-
Hhadydu13 dernière édition par
@mtschoon je n’es pas reusi à résoudre la factorisation car je n’y arrive pas avec des fraction
-
mtschoon dernière édition par mtschoon

Pour terminer la 1), avec l'identité remarquable que je t'ai indiqué, tu obtiens :
(x−92−12)(x−92+12)=0(x-\dfrac{9}{2}-\dfrac{1}{2})(x-\dfrac{9}{2}+\dfrac{1}{2})=0(x−29−21)(x−29+21)=0Tu termines. ( Tu dois trouver x=4x=4x=4 et x=5x=5x=5 )
Pour le minimum , pour la 2) : f(x)f(x)f(x) est de la forme ax2+bx+cax^2+bx+cax2+bx+c
La représentation graphique est une parabole.Si tu le sais (par sûr en Seconde) , avec a>0a\gt 0a>0, le minimum est pour x=−b2ax=-\dfrac{b}{2a}x=−2ab
Si tu ne le sais pas, tu transformes f(x)f(x)f(x) avec la forme canonique précédente
f(x)=2(x2−9x+40)=2((x−92)2−(122)f(x)=2(x^2-9x+40)=2\biggr((x-\dfrac{9}{2})^2-(\dfrac{1}{2}^2\biggr)f(x)=2(x2−9x+40)=2((x−29)2−(212)
f(x)=2((x−92)2−14)\boxed{f(x)=2\biggr((x-\dfrac{9}{2})^2-\dfrac{1}{4}\biggr)}f(x)=2((x−29)2−41)
Tu réfléchis pour quelle valeur de xxx l'expression f(x)f(x)f(x) est minimalePour vérifier tes résultats, tu peux représenter la parabole et tu trouveras graphiquement les réponses à la 1) et à la 2).
-
Hhadydu13 dernière édition par
@mtschoon vous pouvez pas me faire un graphique pour m’indiquer queceque la parabole
-
@hadydu13 Bonjour,
La représentation graphique de la fonction fff :
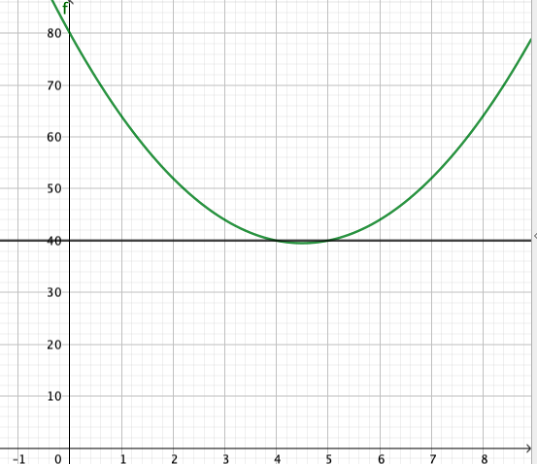
-
Hhadydu13 dernière édition par
@Noemi et du coup comme je fait pour répondre à la 1 et à la 2 avec une parabole ?
-
Pour vérifier les réponses aux questions avec le graphique de la fonction.
Pour la première question, tu traces la droite y=40y= 40y=40 et tu détermines les abscisses des points d'intersection de la droite avec la parabole.
-
Hhadydu13 dernière édition par
@Noemi et la 2?
-
Question 2, Tu traces une droite parallèle à y=40y=40y=40 qui coupe la parabole en un seul point et tu détermines l'abscisse de ce point.
C'est juste une vérification.
-
mtschoon dernière édition par mtschoon

Bonjour,
@hadydu13 , tu poses beaucoup de questions, mais tu ne donnes pas tes réponses...
On ne sait pas trop si tu as vraiment abouti dans les calculs et les raisonnements...Le but est que tu comprennes , pas que tu te contentes de recopier l'aide que l'on te donne.
J'ignore si tu as compris les résultats x=4x=4x=4 et x=5x=5x=5 à la question 1), et si tu as trouvé x=92=4.5x=\dfrac{9}{2}=4.5x=29=4.5 à la question 2) (car je ne te l'avais pas indiqué).
Je te proposais le graphique pour éclairer l'exercice et faire les vérifications (un graphique n'est pas une démonstration).
Noemi t'en as fait un.
Vu les valeurs utiles, ce n'est pas commode...
Je t'en joins un autre en agrandissant la zone où l'on voit les réponses.Réponse de la question 1) correspondant à f(x)=40f(x)=40f(x)=40
La courbe d'équation y=f(x)y=f(x)y=f(x) et la droite d'équation y=40y=40y=40 se coupents au points I(4,40) et J(5,40)
Les solutions cherchées sont bien x=4x=4x=4 et x=5x=5x=5Réponse de la question 2) correspondant à f(x)f(x)f(x) la plus petite possible
Le point le plus bas de la parabole est le point L qui a pour abscisse x=4.5
C'est bien la solution que tu as dû (ou que tu aurais dû) trouver.
L'ordonnée de L , qui est f(4.5)f(4.5)f(4.5) vaut 39,539,539,5 ( mais elle n'est pas demandée dans ton exercice)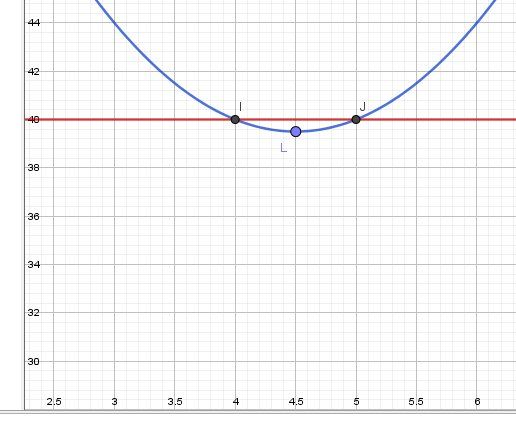
-
mtschoon dernière édition par

@hadydu13 , je te conseille de refaire seul tout l'exercice
C'est la seule façon pour toi de le maîtriser et qui te soit utile pour progresser.Bon travail .