Variations de fonction

Bonjour j’ai un dm à faire et j’ai réussi les deux premières questions mais je n’arrive pas à faire le reste alors j’ai besoin d’aide s’il vous plaît

Une joueuse de handball lance une balle devant elle. Au bout de $x$ mètres parcourus, la hauteur de la balle (en mètres) avant qu’elle ne touche le sol est donnée par :
$h(x) = -0,05x^2 + 0,9x + 2$

Quelle est la hauteur de la balle après 20 mètres parcourus ? Que peut-on en déduire pour la balle ?

a) montrer que $h(x) = -0,05(x-9)^2+6,05$
b) que peut on dire du signe de $x-9)^2$ ?
c) en déduire la hauteur maximale atteinte par la balle.

Donc j’ai fais la 1) et la 2) a) mais je n’arrive pas la b) et c)

Pour la un j’ai fais : $h(20)=-0,05x20^2+0,9x20+2=0$
Au bout de vingt mètres parcourus la hauteur de la balle est de 0 mètres on en déduit donc que la balle est au sol.

Pour la 2) a) :
$0,05x^2+0,9x+2=-0,05(x-9)^2+6,05$
En développant j’ai vu que l’affirmation était vraie

@math58004 Bonjour,

Pour la question 2b),que peut on dire d'une expression au carré ?

@math58004 , bonjour,

Pour le 2)b)

Un carré est toujours positif:

Pour tout $x$ de $R$ : $(x−9)2≥0(x-9)^2\ge 0$

En détaillant :
Pour $x≠9x\ne 9$ : $(x−9)2>0(x-9)^2\gt 0$
Pour $x = 9$ : $x-9)^2 = 0$

2)c) est la conséquence .

Tu sais que $h(x)=-0.05(x-9)^2+6.05$

$(x−9)2≥0(x-9)^2\ge 0$
En mutipliant par $- 0.05$ qui est strictement négafif :
$−0.05(x−9)2≤0-0.05(x-9)^2\le 0$
En ajoutant $6.05$
$−0.05(x−9)2+6.05≤6.05-0.05(x-9)^2+6.05\le 6.05$
$h(x)≤6.05h(x)\le 6.05$

La hauteur maximale atteinte par la balle est donc $6.05$ (m) , obtenue pour $x = 9$

Reposte si ce n'est pas clair.

@Noemi,
Désolée, je n'avais pas vu ta présence lorsque j'ai commencé à répondre...

@mtschoon
Merci beaucoup! Vos explications sont très claires mais je n’ai pas très bien compris la toute dernière comparaison de la 2)c) pouvez vous m’expliquer s’il vous plaît ?

@math58004 , j'explicite la 2)c)

Regarde bien dernière expression de $h (x)$

$x-9)^2$ est positif (au sens large)
Si on détaille
Pour $x = 9$ , $x-9)^2=0$
Pour $x≠9x\ne 9$ , $x-9)^2$ est strictement positif

On multiplie par $- 0.05$
Lorsqu'on multiplie un nombre positif par un nombre négatif , on obtient un nombre négatif
donc $0.05(x-9)^2$ est négatif.( au sens large)
Si l'on détaille :
Pour $x = 9$ , $0.05(x-9)^2=0$
pour $x≠9x\ne 9$ , $0.05(x-9)^2$ est strictement négatif.

On ajoute $6.05$
Donc $0.05(x-9)^2+6.05$ est inférieur à 6.05 (au sens large)
Si l'on détaille :
Pour $x = 9$ , $h(x)=-0.05(x-9)^2+6.05=0+6.05=6.05$
Pour $x≠9x\ne 9$ , $h(x)<6.05h(x)\lt 6.05$ , vu que $h (x)$ est la somme de 6.05 avec un nombre strictement négatif.

Conclusion : la valeur maximale de $h (x)$ est $6.05$ ( valeur obtenue pour $x = 9$ ).

Rergarde tout ça de près.
J'espère que ça ira.

@math58004 , si tu faisais la représentation graphique de la fonction h sur ta calculette, tu trouverais approximativement ceci :

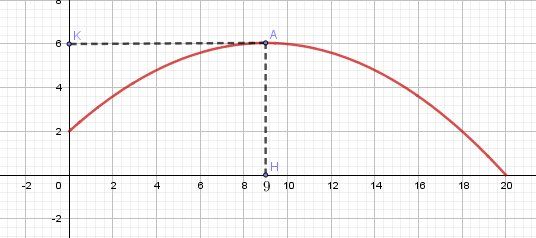
Le sommet est le point A.

Merci beaucoup d’avoir pris le temps de m’expliquer ! Je comprends mieux maintenant

De rien @math58004 et bon DM.