Fonction partie entière
-
Wil Fried dernière édition par

Bonsoir svp j'ai besoin d'un petit éclaircissement.
En fait, j'ai besoin de calculer E[(3n-1)/3], c'est-à-dire la partie entière de ce qui se trouve dans la parenthèse.
Moi j'ai dis que c'était égal à E(n-1/3) qui est égal à E(n)-1/3 qui est égal à n-1/3.
Je l'ai dis en me basant sur la formule qui dit E(x+k)=E(x)+k avec k un entier relatif.Mais dans mon document, ils trouvent plutôt que E[(3n-1)/3]=n-1.
J'aimerais savoir pourquoi ?
-
mtschoon dernière édition par mtschoon

@Wil-Fried , bonsoir,
Comme tu l'indique , la proprité E(x+k)=E(x)+k en valable seulement our k entier.
Tu ne peut pas l'appliquer pour k=13k=\dfrac{1}{3}k=31J'imagine que nnn est entier.
La réponse de ton document est tout à fait exacte.
Il faur encadrer n−13n-\dfrac{1}{3}n−31 par deux entiers consécutifs.−1≤−13<0-1\le -\dfrac{1}{3}\lt 0−1≤−31<0
En ajoutant n à chaque membre :
n−1≤n−13<nn-1\le n-\dfrac{1}{3}\lt nn−1≤n−31<nPar définition : E(n−13)=n−1E(n-\dfrac{1}{3})=n-1E(n−31)=n−1
C'est à dire E(3n−13)=n−1E(\dfrac{3n-1}{3})=n-1E(33n−1)=n−1
-
Wil Fried dernière édition par

@mtschoon Svp, pourquoi par définition E(n-13\frac{1}{3}31)= n-1 ?? Je ne comprend pas.
-
Wil Fried dernière édition par

@Wil-Fried Ah oui je comprend! Vous vous êtes servies de votre encadrement.
Maintenant j'aimerais savoir pourquoi dites-vous que -1 est inférieur ou égal à -1/3 ? Pourtant -1 est strictement inférieur à -1/3.
-
mtschoon dernière édition par mtschoon

C'est pour appliquer la définition exacte de partie entière .
Comme tu peux voir, j'ai mis ≤\le≤ à gauche et <\lt< à droite.
Définition : Soit xxx un réel quelconque .
Il existe un entier nnn tel que n≤x<n+1n\le x\lt n+1n≤x<n+1
Par définition E(x)=nE(x)=nE(x)=n (c'est l'entier de gauche de la double inégalité)Bien sûr , dans le cas que tu proposes, ce n'est pas indipensable, mais cette définition permet de pourvoir s'appliquer à tout réel, même entier.
Par exemple, si l'on cherche E(2)E(2)E(2)
2≤2<32\le 2\lt 32≤2<3 => E(2)=2E(2)=2E(2)=2
-
Wil Fried dernière édition par

@mtschoon Je vois, merci beaucoup
-
Wil Fried dernière édition par

@mtschoon On me demande de calculer S( de 1 à 100 ) de la partie entière de k/2.
J'ai pensé à séparer les termes selon la parité de leur indices.
Comme dans la formule de séparation l'indice commence par 0, alors j'ai fais un décalage d'indice pour pouvoir avoir 0 aussi dans mon exercice.
J'obtiens donc S( de 0 à 99 ) de la partie entière de (k+1)/2.J'ai alors appliqué la formule et après tout cela j'obtiens comme résultat final 2499.
J'aimerais savoir si c'est juste mon résultat ?
-
@Wil-Fried Bonsoir,
Vérifie le calcul, je trouve 2500.
-
Wil Fried dernière édition par

@Noemi 1225+1225+49 c'est le dernier résultat que je trouve.
-
Comment as-tu procédé ?
Avec les nombres impairs, S2=1+2+....+50S_2=1+2+ ....+50S2=1+2+....+50
Avec les nombres pairs, S1=1+2+....+49S_1=1+2+ ....+49S1=1+2+....+49
La somme :....
-
Wil Fried dernière édition par

@Noemi, Voici comment j'ai procédé :
S= ∑k=1100⌊k2⌋\sum_{k=1}^{100}\left\lfloor\dfrac{k}{2}\right\rfloor∑k=1100⌊2k⌋
S=∑k=099⌊k+12⌋\sum_{k=0}^{99}\left\lfloor\dfrac{k+1}{2}\right\rfloor∑k=099⌊2k+1⌋
S=∑k=0[992]⌊2k+12⌋+∑k=0[982]⌊2k+22⌋\sum_{k=0}^{[\frac{99}{2}]}\left\lfloor\dfrac{2k+1}{2}\right\rfloor+\sum_{k=0}^{[\frac{98}{2}]}\left\lfloor\dfrac{2k+2}{2}\right\rfloor∑k=0[299]⌊22k+1⌋+∑k=0[298]⌊22k+2⌋
S=∑k=049⌊k+12⌋\sum_{k=0}^{49}\left\lfloor{k+\frac{1}{2}}\right\rfloor∑k=049⌊k+21⌋+∑k=049⌊k+1⌋\sum_{k=0}^{49}\left\lfloor{k+1}\right\rfloor∑k=049⌊k+1⌋
Je détermine alors la partie entière de k+12k+\frac{1}{2}k+21 et de k+1k+1k+1
Celle de k+1k+1k+1 est k+1k+1k+1 et celle de k+12k+\frac{1}{2}k+21 est kkkS=∑k=049k+∑k=049(k+1)\sum_{k=0}^{49}k+\sum_{k=0}^{49}(k+1)∑k=049k+∑k=049(k+1)
S=50×(0+49)2\frac{(0+49)}{2}2(0+49)+50×(0+49)2\frac{(0+49)}{2}2(0+49)+∑k=0491\sum_{k=0}^{49}1∑k=0491
S=1225+1225+491225+1225+491225+1225+49
S=249924992499
-
La dernière somme est égale à 50, car de 0 à 49, tu as 50 valeurs.
-
Wil Fried dernière édition par

@Noemi Ah d'accord. Merci beaucoup!
-
mtschoon dernière édition par mtschoon

Bonjour,
Désolée @Wil-Fried , hier soir je n'étais pas connectée.
Effectivement, je viens de faire mon calcul (un peu différemment, en regroupant les termes deux par deux, sauf le premier et le dernier) et j'obtiens 250025002500
-
Wil Fried dernière édition par

Bonjour @mtschoon, Merci encore!
-
mtschoon dernière édition par mtschoon

De rien @Wil-Fried, on fait au mieux.
J'espère que la fonction "partie entière" ne te pose plus de problème.
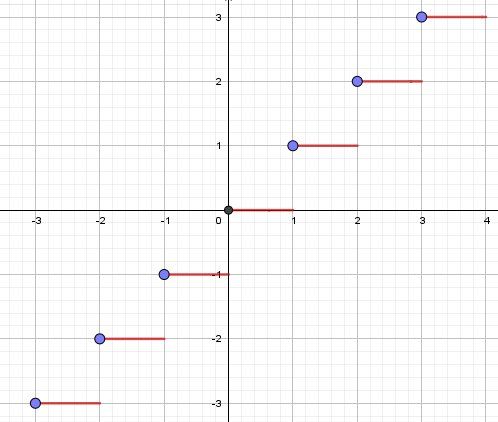
Je t'indique ( ce qui est peut-être dans ton cours ) la représentation graphique (partielle) de cette fonction : définie sur RRR, en escalier (constante par intervalle).
Elle est composée de segments parallèles à l'axe des abscisses, (fermés à gauche par un point et ouverts à droite).
Bon travail.
-
Wil Fried dernière édition par

@mtschoon C'est génial! Merciii
-
mtschoon dernière édition par

De rien @Wil Fried
