Aire des carrés parties coloriées

[evann]

Bonjour :

Voici mon énoncé :
Les 3 carrés sont égaux et mesurent 1cm de cotes .
Quelles est l air de la partie coloriée ? ))

[evann]

@evann

Pour les carrés 1 et 3 , je dirai que l aire est (1*0,5)/2=0,25 cm2 pour le carré 1 et le 3 .

[Noemi]

@evann Bonjour,

Ton calcul correspond à l'aire coloriée dans les carrées 1 et 3.
Tu peux utiliser un repère et calculer les coordonnées du point d'intersection située dans le carré 2.

[mtschoon]

Bonjour,

Si ça peut aider à faire les calculs, je joins un schéma avec des notations pour pouvoir s'expliquer clairement.

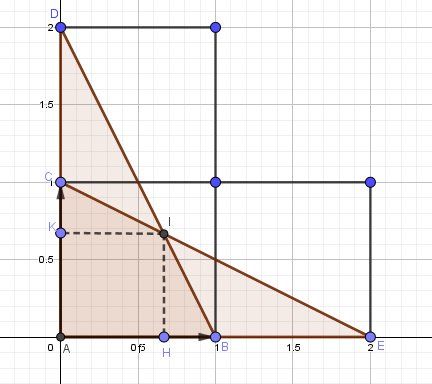
Le repère choisi est $(A,\overrightarrow{AB},\overrightarrow{AC})$

[evann]

@mtschoon
Je dois chercher les coordonnés du point I ?

[Noemi]

@evann

Oui, cherche les coordonnées du point I.
Détermine d'abord les équations des droites $(BD)$ et $(CE)$;

Autre méthode, tu peux utiliser la propriété de Thalès pour déterminer la valeur de $IH$ ou $IK$.
Puis tu calcules l'aire du triangle $IBE$.

[evann]

@Noemi
Alors j ai trouve pour équation de la droite (DB)
Y=-2x+2
Et pour la droite (CE)
Y=_1/2X+3/4

[Noemi]

@evann

L'équation de la droite (CE) est : $y=-\frac{1}{2}x+1$

Détermine les coordonnées du point I.

[evann]

@Noemi
Oui , je viens de m en rendre compte car je trouvais un point I ( non concordant )
J ai donc fait -1/2X+1=-2x+2
x=2/3 et donc y =2/3

[Noemi]

@evann

Tu peux calculer maintenant l'aire du triangle $ABD$ et l'aire du triangle $IBE$ puis faire la somme.

J'ai indiqué dans un précédent post une autre méthode : Utiliser la propriété de Thalès pour déterminer la mesure de $IH$.

[evann]

@Noemi

Je trouve 7/3 cm2

[Noemi]

@evann

La réponse est $\frac{4}{3}$, vérifie le calcul.
Aire du triangle $ABD$ : ....
Aire du triangle $IBE$ : ....
Somme : ....

[mtschoon]

Bonjour,
@evann , j'espère que tu es arrivé à obtenir la réponse $\frac{4}{3}$ que t'a donnée Noemi.

$aire{d}^{\prime }untriangle=\frac{base\times hauteur}{2}$

donc $aire(ABD)=\frac{AB\times AD}{2}$ tu dois trouver $1(c{m}^2)$

Pour trouver l'aire de $(IBE)$, tu peux prender pour base $BE$ et pour hauteur $IH$
Cette hauteur $IH$ est égale à l'ordonnée de I que tu as calculée et qui vaut $\frac{2}{3}(cm)$
(C'est pour cela qu'il a fallu trouver les coordonnées de I)

donc $aire(IBE)=\frac{BE\times IB}{2}$ tu dois trouver $\frac{1}{3}(c{m}^2)$

Conclusion :
L'aire de la partie colorée (pour éviter bien sûr, de prendre des parties qui se superposent) vaut $aire(ABD)+aire(IBE)$ , ce qui fait $\frac{4}{3}(c{m}^2)$, comme attendu.

J'espère que tu as tout compris.

[evann]

@mtschoon
Bonjour ,
J ai calculé HIE et j ai déduis l aire HIB .
Mais j arrive à retrouver ´ aire de Noémie , j avais fait une erreur de calcul .
Merci à tous les deux

[mtschoon]

@evann ,

C'est un peu plus long de calculer l'$aire(HIE$) pour déduire l'$aire(HIB)$ mais si tu préfères ainsi pour te ramener à des triangles rectangles , ça va très bien.

Donc, tout est OK pour toi. C'est parfait.