DM math , j’ai besoin d’aide pour qu’elle que question
-
Cclea55 dernière édition par Noemi
bonjour à tous j’aimerais recevoir de l’aide pour un DM de math que j’ai à faire .
Je n’arrive pas à faire 4 des questions :
la question 2 et 3 de l’exercice 2
et les questions 2 et 3 de l’exercice 3 .si quelqu’un saurais m’aider


- élément de liste
Scan supprimé par la modération.
-
@clea55 Bonsoir,
Le scan de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, figures ou graphiques sont autorisés.
Ecris l'énoncé et tu obtiendras des pistes de résolution.
Un seul exercice par post.
Le scan va être supprimé.
-
Cclea55 dernière édition par
je met l’énoncer des questions du dm que je en comprends pas :
- calculer les coordonnées des vecteurs AB et BC.
2.en déduire les coordonnées du vecteur 2AB-3BC.
3.soit M(x;y) un point tel que (vecteurs)AM= 2AB-3BC.
calculer les coordonnées du point M.j’ai trouvé la réponse à la question 1 mais je ne sais pas comment faire les autres
-
Il faut écrire l'énoncé en entier. Sans les données, il est impossible d'indiquer des éléments de réponse.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Noemi a dit dans DM math , j’ai besoin d’aide pour qu’elle que question :
Il faut écrire l'énoncé en entier. Sans les données, il est impossible d'indiquer des éléments de réponse.
Effectivement !
En parcourant le web, je suis tombée sur un énoncé demandant les mêmes questions 2) et 3) avec des coordonnées pour A,B,C.
J'ignore si les coordonnées ainsi trouvées sont ceux de cet énoncé , mais pour ne pas conserver ce topic inutilement, pour consultation éventuelle, je mets des pistes de calculs avec ces coordonnées.
-
mtschoon dernière édition par

Pistes de calcul,
A(2,−3);B(1,−1);C(4,5)A(2,-3) ; B(1,-1) ; C(4,5)A(2,−3);B(1,−1);C(4,5)
AB→ (xB−xA,yB−yA)=(1−2,−1+3)=(−1,2)\overrightarrow{AB}\ (x_B-x_A,y_B-y_A)=(1-2,-1+3)=(-1,2)AB (xB−xA,yB−yA)=(1−2,−1+3)=(−1,2)
BC→ (xC−xB,yC−yB)=(4−1,5+1)=(3,6)\overrightarrow{BC}\ (x_C-x_B,y_C-y_B)=(4-1,5+1)=(3,6)BC (xC−xB,yC−yB)=(4−1,5+1)=(3,6)Conséquences :
2AB→ (−2,4)2\overrightarrow{AB}\ (-2,4)2AB (−2,4)
3BC→ (9,18)3\overrightarrow{BC}\ (9,18)3BC (9,18)
2AB→−3BC→ (−11,−14)2\overrightarrow{AB}-3\overrightarrow{BC}\ (-11,-14)2AB−3BC (−11,−14)
Donc
AM→ (−11,−14)\overrightarrow{AM}\ (-11,-14)AM (−11,−14)
xM−xA=−11x_M-x_A=-11xM−xA=−11 <=> xM=−11+xA=−9x_M=-11+x_A=-9xM=−11+xA=−9
yM−yA=−14y_M-y_A=-14yM−yA=−14 <=> yM=−14+yA=−17y_M=-14+y_A=-17yM=−14+yA=−17
-
mtschoon dernière édition par

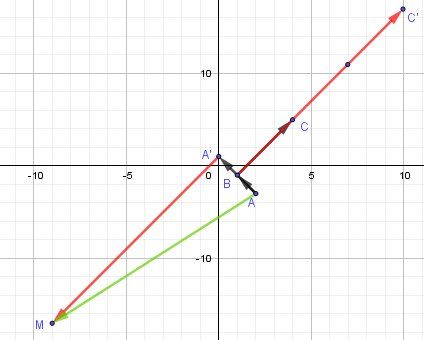
Graphique :
AA′→=2AB→\overrightarrow{AA'}=2\overrightarrow{AB}AA′=2AB
BC′→=3BC→\overrightarrow{BC'}=3\overrightarrow{BC}BC′=3BC
AA′→−BC′→=AA′→+C′B→=AM→\overrightarrow{AA'}-\overrightarrow{BC'}=\overrightarrow{AA'}+\overrightarrow{C'B}=\overrightarrow{AM}AA′−BC′=AA′+C′B=AMOn obtient : M(−9,−17)M(-9,-17)M(−9,−17)
Bonne consultation éventuelle.