Etude d'une fonction trigonométrique
-
Alef Education dernière édition par Noemi
)Bonjour
j'ai besoin de votre aide pour résoudre cet exercice.
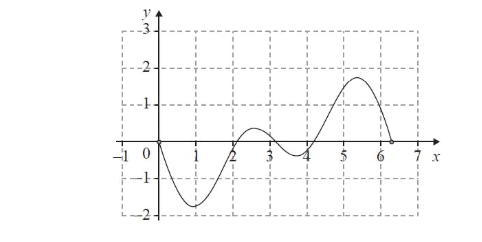
On considère la fonction f définie sur l’intervalle [0 ; 2π] par : f (x) = cos x + Cos(2x) + 1.
La courbe préconstruite ci-dessous est la représentation graphique de la fonction dérivée f 'sur l’intervalle [0 ; 2π].- a) Déterminer la fonction dérivée f ′ de la fonction f.
b) Montrer que, pour tout nombre réel x de l’intervalle [0 ; 2π] :
f ′(x) = – sin(x) [1 + 2cos(x)]. 2. Résoudre dans l’intervalle [0 ; 2π], l’équation produit : sin(x) [1 + 2cos(x)] = 0. - a) En s’appuyant sur la représentation graphique de la fonction dérivée
f ′ ci-dessus, dresser le b) Déduire des questions 2. et 3. a) le tableau de variations de la fonction f sur l’intervalle [0 ; 2π].
tableau de signes de f ′(x) sur l’intervalle [0 ; 2π].
Préciser les ordonnées des points dont l’abscisse x vérifie f ′(x) = 0 . - Tracer la courbe représentative de f sur l’intervalle [0 ; 2π] dans le repère précédent (où f ′est déjà représentée).
- a) Déterminer la fonction dérivée f ′ de la fonction f.
-
@Alef-Education Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
La dérivée de cos(x)cos(x)cos(x) est −sin(x)-sin(x)−sin(x)
celle de cos(u(x))cos(u(x))cos(u(x)) est −u′(x)sin(u(x))-u'(x)sin(u(x))−u′(x)sin(u(x))
-
DDavS dernière édition par
@Alef-Education c'est bizarre parce que je trouve que la dérivée est égale à :
f'(x)=-sin(x)[1+4cos(x)]
-
mtschoon dernière édition par mtschoon

Bonjour,
@DavS a dit dans Besoin d'aide pour résoudre un exercice :
@Alef-Education c'est bizarre parce que je trouve que la dérivée est égale à :
f'(x)=-sin(x)[1+4cos(x)]Tout à fait d'accord avec toi @Alef-Education
f′(x)=−sinx−2sin(2x)=−sinx−2(2sincosx)f'(x)=-sinx-2sin(2x)=-sinx-2( 2sincosx)f′(x)=−sinx−2sin(2x)=−sinx−2(2sincosx)
f′(x)=−sinx−4sinxcosx=−sinx(1+4cosx)f'(x)=-sinx-4sinxcosx=-sinx(1+4cosx)f′(x)=−sinx−4sinxcosx=−sinx(1+4cosx)Quelquechose ne va pas dans cet énoncé...
-
mtschoon dernière édition par mtschoon

Je viens de chercher où pouvait être l'erreur d'énoncé.
Pour obtenir la dérivée proposée f′(x)=−sinx(1+2cosx)f'(x)=-sinx(1+2cosx)f′(x)=−sinx(1+2cosx), il faudrait que l'énoncé soit, par exemple :
f(x)=cosx+12cos(2x)+1\boxed{f(x)=cosx+\dfrac{1}{2}cos(2x)+1}f(x)=cosx+21cos(2x)+1
( bien sûr, au lieu du "1" on pourrait mettre une autre valeur réelle)
Ainsi :
f′(x)=−sinx+12(−sin(2x))×2f'(x)=-sinx+\dfrac{1}{2}(-sin(2x))\times 2f′(x)=−sinx+21(−sin(2x))×2
f′(x)=−sinx−sin(2x)=−sinx−2sinxcosxf'(x)=-sinx-sin(2x)=-sinx-2sinxcosxf′(x)=−sinx−sin(2x)=−sinx−2sinxcosx
f′(x)=−sinx(1+2cosx)f'(x)=-sinx(1+2cosx)f′(x)=−sinx(1+2cosx)
-
Alef Education dernière édition par Alef Education
Je m'excuse, là c'est marqué f(x)=1/2 cos x+Cos(2x)+1
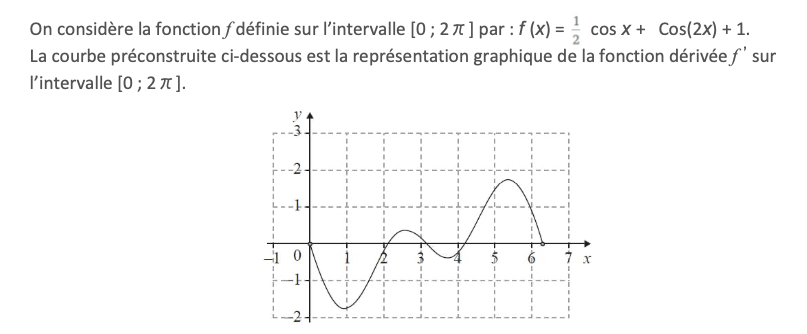
Donc là je suppose qu'il y a une erreur au niveau du 1/2 (une question piège) !!!
Donc la fonction est plutot f(x) = cos x+1/2 cos(2x)+1. Dans ce cas là on aura bine le résultat. Pour laquestion résoudre l'équation sin(x) [1 + 2cos(x)] = 0 on aura sin x=0 ou cos x=-1/2 alors les solutions sont les valeurs 0, π\piπ et 2π\piπ/3, n'est ce pas ?
-
mtschoon dernière édition par mtschoon

Bonsoir @Alef-Education ,
Effectivement, la seconde expression (de l'énoncé ) que tu donnes ne convient pas avec la dérivée indiquée.Piège ? ou erreur d'énoncé (plus probable...) ?
Je ne vois pas d'autre solution que de prendre la fonction que je te propose et avec ça, toute la suite est valable.
-
mtschoon dernière édition par

Pour trouver les solutions qui annulent le dérivée, fais le cercle trigonométrique et utilise les angles remarquables
Sur [0,2π][0,2\pi][0,2π]
sinx=0sinx=0sinx=0 apour x=0,π,2πx=0,\pi, 2\pix=0,π,2π
cosx=−12cosx=-\dfrac{1}{2}cosx=−21 pour x=2π3,4π3x=\dfrac{2\pi}{3},\dfrac{4\pi}{3}x=32π,34πVérifie que ces valeurs correspondent au graphique.
-
Alef Education dernière édition par
Merci. La suite de l'exercice:
- a) En s’appuyant sur la représentation graphique de la fonction dérivée
f ′ ci-dessus, dresser le le tableau de variations de la fonction f sur l’intervalle [0 ; 2π].
b) Déduire des questions 2. et 3. a) le tableau de variations de la fonction f sur l’intervalle [0 ; 2π]. Préciser les ordonnées des points dont l’abscisse x vérifie f ′(x) = 0 . - Tracer la courbe représentative de f sur l’intervalle [0 ; 2π] dans le repère précédent (où f ′est déjà représentée)
- a) En s’appuyant sur la représentation graphique de la fonction dérivée
-
Alef Education dernière édition par Alef Education
C'est bien ca le tableau de variation
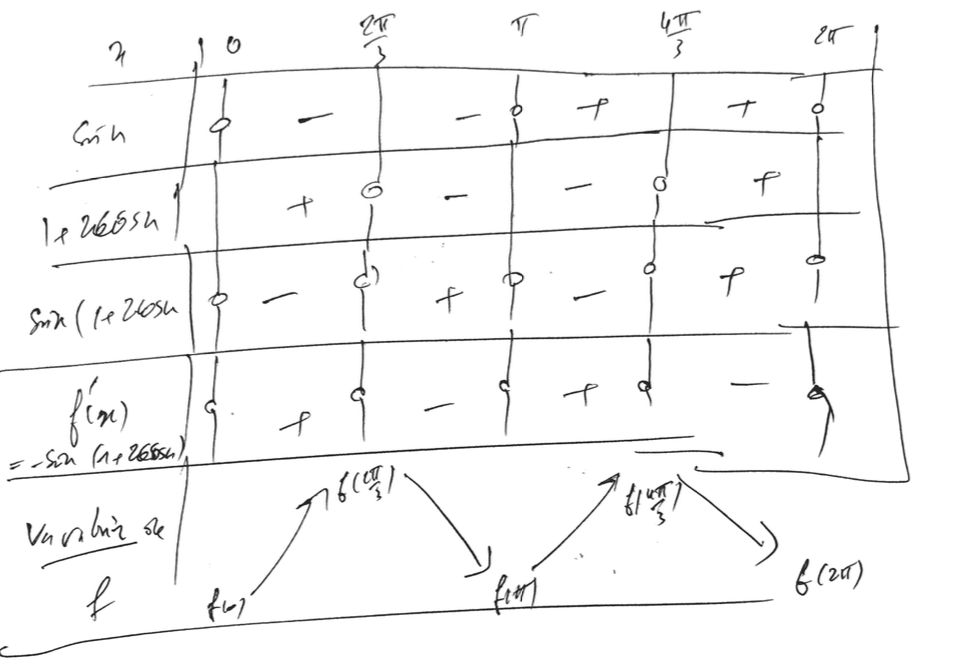
avec f(0)=5/2, f(2π\piπ/3)=1/4, f(π\piπ)=1/2, f(4π\piπ/3)=1/4 et f(2π\piπ)=5/2
-
mtschoon dernière édition par mtschoon

Ce n'est pas clair entre sinx(1+2cosx) et -sinx(1+2cosx)
Il y a des confusions entre sinx et -sinx
-
Alef Education dernière édition par
MAis la fonction ne peut pas etre croissante de 5/2 vers 1/4. Non?
-
mtschoon dernière édition par mtschoon

f′(x)=−sinx(1+2cosx)f'(x)=-sinx(1+2cosx)f′(x)=−sinx(1+2cosx)
il doit y avoir des problèmes avec le signe "-"
-
Alef Education dernière édition par
@mtschoon Mais j'ai bien inversé les signes sans f et j'ai pris le "-" en considération.
-
mtschoon dernière édition par mtschoon

@Alef-Education, le signe de f'(x) que tu trouves devrait correspondre au graphique donné (pour la dérivée).
Avec les écritures manuelles que tu utilises, ce n'est pas clair...
Demain je te ferais un tableau de variation précis pour éviter toute confusion.
-
Alef Education dernière édition par
@mtschoon ainsi que la courbe représentative. Merci.
-
mtschoon dernière édition par mtschoon

@Alef-Education , bonjour,
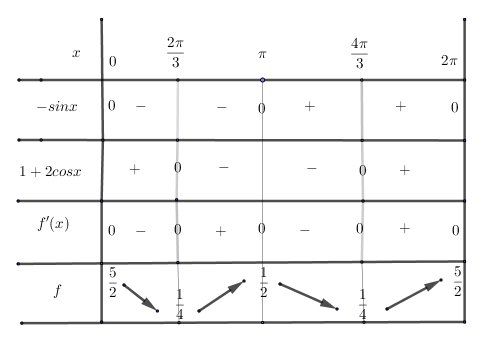
Comme convenu, je te joins un tableau de variation, pour que tu puisses vérifier/modifier le tien.
Le signe de (−sinx)(-sinx)(−sinx) et (1+2cosx)(1+2cosx)(1+2cosx) se lit sur le cercle trigonométrique.
Le signe de f′(x)f'(x)f′(x) s'obtient, en utilisant la règle des signes relative au produit, avec le signe de chaque facteur (−sinx)(-sinx)(−sinx) et (1+2cosx)(1+2cosx)(1+2cosx).
Le sens de variation de fff s'en déduit.Demande si tu as quelque chose qui te gène.
-
mtschoon dernière édition par mtschoon

@Alef-Education , vu que tu le souhaites, je te mets le graphique.
Tu peux l'obtenir sur ta calculette.
La fonction dérivée f′f'f′ est en bleu et la fonction fff est en rouge.Il faut bien sûr que tu réalises (c'est le but), que lorsque la courbe dérivée est en dessous de l'axe des abscisses, f′(x)f'(x)f′(x) est négative donc f est décroissante et que lorsque la courbe dérivée est au dessus de l'axe des abscisses, f′(x)f'(x)f′(x) est positive donc f est croissante
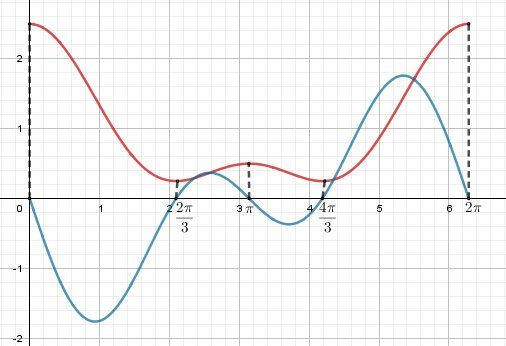
-
Alef Education dernière édition par
Merci beaucoup, puis-je mettre un deuxième exercice ?
-
@Alef-Education Bonsoir,
Oui, tu peux proposer un autre exercice, mais écris l'énoncé et tes éléments de réponse.
-
Alef Education dernière édition par
@Noemi D accord. Merci