DM suites géométriques

Bonjour, je n’arrive pas à faire ce DM, j’aimerai vraiment avoir votre aide s’il vous plaît.

Soit (Un) la suite définie par la relation de récurrence :
On dit que (Un) est une suite géométrique de premier terme u et de raison q.

1° a) Etude d'un exemple: on pose u = 0.5 et q = 2

-Calculer les 5 premiers termes de la suite
-Représenter le nuage de points (n; un) pour O< n $ 5
-Donner une expression de Un en fonction de n

b) Cas général : compléter :
Un = u0 q
Un = u1 q
Un = Up q
avec p < n

2° Déterminer, suivant les valeurs de q , les variations de (Un).
3° On note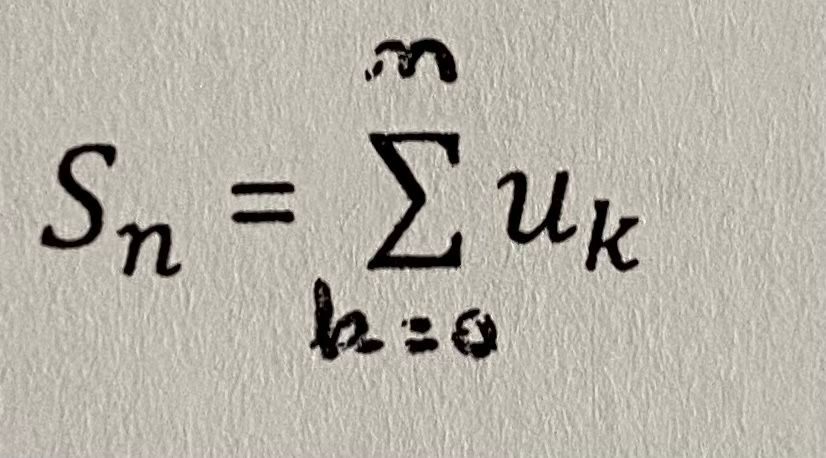
a) Calculer Sn - q Sn, puis en déduire Sn, en fonction de U0 et q. (on distinguera 2 cas....)
b) Calculer, en détaillant votre démarche, S = 1 + 2 + 4 +....... + 64

4° Applications

A )
Un concours scientifique est organisé depuis 2015; les filles ne représentaient alors qu'un quart des participants. Entre 2015 et 2019, on a constaté une augmentation moyenne annuelle de la proportion de filles participant à ce concours de 12 %. On extrapole que la proportion de filles va continuer à progresser ainsi pendant dix ans.

a. Quelle était la proportion de filles en 2016 ?
b. Quelle serait alors la proportion de filles en 2021
(arrondir au millième) ?
c. Pour tout nombre entier naturel n, on note pn la proportion de filles l'année 2015 + n.
Pour n < 10, exprimer Pn+ 1 en fonction de Pn
d. En déduire la nature de la suite (Pn) et en préciser
les valeurs utiles.
On donne la fonction en Python suivante.
Quelle est la valeur de proportionfilles(0.5)?
Interpréter le résultat.

B)
Dans une entreprise, on propose deux contrats d'em-
bauche au 1er janvier.
Contrat de type A : un salaire mensuel net de début de contrat de 1 600 €, puis une augmentation de 70 €
chaque année.
Contrat de type B: un salaire mensuel net de début
de contrat de 1 300 €, puis une augmentation de 6 %
chaque année.
On note A0, le salaire mensuel net de début de contrat pour le contrat A, et An le salaire net après n années, où n est un nombre entier naturel.
De même, on note B, le salaire après n années pour le
contrat B.

Pour tout nombre entier naturel n, écrire une relation liant les termes An et An + 1, puis une relation liant Bn et Bn+1, et en déduire la nature des suites (An) et (Bn).
2° Ecrire un algorithme en Python qui détermine au bout de combien d'années le salaire du contrat B aura dépassé celui du contrat A. Donner cette valeur.

C)
On définit (Un) par : U = 0 et Un+1
=- 0.5Un + 1; et (Vn) par : Vn = Un - 2/3

1° Calculer u1, U2, U3, u4 et u5.
2° Montrer que (Vn) est une suite géométrique dont on donnera les éléments.
3° En déduire Vn puis Un en fonction de n. Retrouver le calcul de u5.

@julielatortue Bonjour,

Un seul exercice par post, donc propose les applications dans d'autres posts.

Pour le début, indique tes éléments de réponse et la question qui te pose problème.

Bonjour,

@julielatortue , la première partie de ton exercice est relative aux propriétés des suites géométriques.

Je pense que tu dois trouver tous les éléments utiles ici au paragraphe IV (définition, propriétés, Somme)

https://www.mathforu.com/premiere-s/les-suites-en-1ere-s/