calcul de probabilités
-
Livindiam Livin dernière édition par

Bonjour
J'aimerais savoir si mon raisonnement pour un calcul de probabilité est correct
Dans une population , si on est vacciné, la probabilité de tomber malade est de 1%
Si on n'est pas vacciné, la probabilité de tomber malade est de 15%
3,52% de la population est malade
V:"La personne est vacciné" et M:"La personne est malade" sont les deux évènements.Je dois calculer p(V)
Je me suis basée sur pM(V)=0,1 , utilisé la formule p(VinterM)/p(M) = pM(V) avec p(V)=p et p(Vbarre)=1-p
Le résultat final pour p est environ 0,14
En espérant que les démarches effectués sont plutôt claires
-
mtschoon dernière édition par mtschoon

-
Livindiam Livin dernière édition par

@mtschoon Re bonjour, j'ai revérifié et c'est bien l'énoncé qu'on me donne
En revanche je me rends compte d'une erreur faite de ma part : pM(V)=0,01 car 1/100=0,01 et non 0,1 tel que je l'ai écrit...
-
Livindiam Livin dernière édition par

@Livindiam-Livin De même pour 3,52% qui donne p(M)=0,0352 ...
-
mtschoon dernière édition par mtschoon

Tu as donc, avec les données de ton énoncé :
pV(M)=0.01p_V(M)=0.01pV(M)=0.01
pV‾(M)=0.15p_{ \overline{V}} (M)=0.15pV(M)=0.15
p(V)=pp(V)=pp(V)=p
p(V‾)=1−pp(\overline{V})=1-pp(V)=1−p
En faisant un arbre pour résumer tout ça :
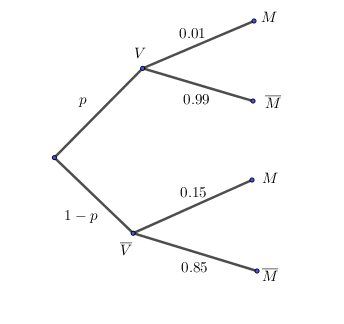
p(M)=p(0.01)+(1−p)(0.15)p(M)=p(0.01)+(1-p)(0.15)p(M)=p(0.01)+(1−p)(0.15)
-
Livindiam Livin dernière édition par

@mtschoon La probabilité de tomber malade étant de 3,52%, p(M)=0,0352
Je me suis mal exprimée
-
Livindiam Livin dernière édition par

@mtschoon J'ai réessayé de résoudre cette exercice
J'ai repris la frome pM(V)=0,01 de l'arbre et continuer en faisant p(MinterV)/p(M)=0,01 et changer le tout. Je finis par trouver que p est environ égale à 0,13
-
Livindiam Livin dernière édition par

@mtschoon a dit dans calcul de probabilités :
Tu as donc, avec les données de ton énoncé :
pV(M)=0.01p_V(M)=0.01pV(M)=0.01
pV‾(M)=0.15p_{ \overline{V}} (M)=0.15pV(M)=0.15
p(M)=0.352p(M)=0.352p(M)=0.352
p(V)=pp(V)=pp(V)=p
p(V‾)=1−pp(\overline{V})=1-pp(V)=1−p
En faisant un arbre pour résumer tout ça :

p(M)=p(0.01)+(1−p)(0.15)p(M)=p(0.01)+(1-p)(0.15)p(M)=p(0.01)+(1−p)(0.15)
J'ai toujours un doute sur les données.
Les données qu'on me donne sont les suivantes :
Dans une population :
Si on est vacciné, la probabilité de tomber malade est de 1%
Si on ne l'est pas (vacciné je suppose), la probabilité de tomber malade est de 15%
On constate que 3,52% de la population est malade
déterminer p(V) (la personne est vacciné)
-
mtschoon dernière édition par mtschoon

Re-bonjour @Livindiam-Livin
Merci pour les données vérifiées. La valeur de p(M)p(M)p(M) me faisait douter, mais après calcul, c'est bon.
Donc p(M)=0.0352p(M)=0.0352p(M)=0.0352
Tu dois résoudre p(M)=p(0.01)+(1−p)(0.15)p(M)=p(0.01)+(1-p)(0.15)p(M)=p(0.01)+(1−p)(0.15)
0.0352=p(0.01)+(1−p)(0.15)0.0352=p(0.01)+(1-p)(0.15)0.0352=p(0.01)+(1−p)(0.15)
Tu développes :
0.0352=p(0.01)++0.15−0.15p0.0352=p(0.01)++0.15-0.15p0.0352=p(0.01)++0.15−0.15p
Tu transposes :
0.15p−0.01p=0.15−0.03520.15p-0.01p=0.15-0.03520.15p−0.01p=0.15−0.0352
Tu termines et , sauf erreur, tu dois trouver : p=0.82p=0.82p=0.82
Bon calcul.
-
Livindiam Livin dernière édition par

@mtschoon Je vais essayer
Quel donnée pourrait être erroné ? Y'a t-il peut-être une autre manière de déterminer p(V) ?
Merci pour l'aide déjà apporté
-
mtschoon dernière édition par mtschoon

@Livindiam-Livin , c'est la valeur de p(M)p(M)p(M) qui me faisant douter (car j'avais mal lu), mais comme indiqué, c'est cohérent.
Je regarde la proposition précédente que tu avais indiquée :
@Livindiam-Livin a dit dans calcul de probabilités :
@mtschoon J'ai réessayé de résoudre cette exercice
J'ai repris la frome pM(V)=0,01 de l'arbre et continuer en faisant p(MinterV)/p(M)=0,01 et changer le tout. Je finis par trouver que p est environ égale à 0,13
çe n'est pas bon car dans ta formule, il y confusion entre M et V
C'est une probabilité conditionnelle sachant V
pV(M)=p(M∩V)p(V)=0.01p_V(M)=\dfrac{p(M\cap V)}{p(V)}=0.01pV(M)=p(V)p(M∩V)=0.01
0.130.130.13 n'est donc pas une bonne réponse.La démarche que je t'ai proposée me semble être la seule possible.
-
Livindiam Livin dernière édition par

@mtschoon a dit dans calcul de probabilités :
@Livindiam-Livin , c'est la valeur de p(M)p(M)p(M) qui me faisant douter (car j'avais mal lu), mais comme indiqué, c'est cohérent.
Je regarde la proposition précédente que tu avais indiquée :
@Livindiam-Livin a dit dans calcul de probabilités :
@mtschoon J'ai réessayé de résoudre cette exercice
J'ai repris la frome pM(V)=0,01 de l'arbre et continuer en faisant p(MinterV)/p(M)=0,01 et changer le tout. Je finis par trouver que p est environ égale à 0,13
çe n'est pas bon car dans ta formule, il y confusion entre M et V
C'est une probabilité conditionnelle sachant V
pV(M)=p(M∩V)p(V)=0.01p_V(M)=\dfrac{p(M\cap V)}{p(V)}=0.01pV(M)=p(V)p(M∩V)=0.01
0.130.130.13 n'est donc pas une bonne réponse.La démarche que je t'ai proposée me semble être la seule possible.
Je retravaille tout ça merci pour l'aide !
-
mtschoon dernière édition par

De rien @Livindiam-Livin et bon travail.
Si tu comprends bien la construction de l'arbre probabiliste, tout s'éclairera. C'est la démarche usuelle.
-
mtschoon dernière édition par mtschoon

@Livindiam-Livin , une remarque,
L'arbre est la conséquence des propriétés des probabilités.
L'utiliser est plus simple qu'écrire les formules (c'est le but), mais si tu préfères, tu peux rédiger autrement (sans te servir de l'arbre).
M=(M∩V)∪(M∩V‾)M=(M\cap V)\cup (M\cap \overline{V})M=(M∩V)∪(M∩V)
M∩VM\cap VM∩V et M∩V‾M\cap \overline{V}M∩V sont disjoints, donc :
p(M)=p(M∩V)+p(M∩V‾)p(M)=p(M\cap V)+p(M\cap \overline{V})p(M)=p(M∩V)+p(M∩V)
p(M)=[p(V)×pV(M)]+[p(V‾)×pV‾(M)]p(M)=[p(V)\times p_V(M)]+[p(\overline V)\times p_{\overline V}(M)]p(M)=[p(V)×pV(M)]+[p(V)×pV(M)]
d'où :
p(M)=[p×0.01]+[(1−p)×0.15]p(M)=[p\times 0.01]+[(1-p)\times 0.15]p(M)=[p×0.01]+[(1−p)×0.15]
0.0352=0.01p+0.15(1−p)0.0352=0.01p+0.15(1-p)0.0352=0.01p+0.15(1−p)
0.0352=0.01p+0.15−0.15p0.0352=0.01p+0.15-0.15p0.0352=0.01p+0.15−0.15p
Tu termines la résolution et tu trouves p=0.82p=0.82p=0.82
Bon calcul.