Besoin de vos remarques

[Alef Education]

Bonsoir, j'ai besoin de vos commentaires et vos remarques par rapport à ces réponses.

Merci de corriger cette copie de l’élève, et lui donner une explication à chacune de ses réponses !

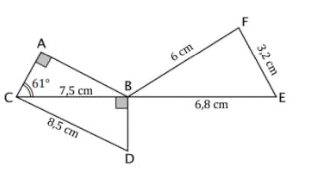
La figure ci-contre n’est pas représentée en vraie grandeur. Les points C, B et E sont alignés. Le triangle ABC est rectangle en A. Le triangle BDC est rectangle en B.

1. Montrer que la longueur BD est égale à 4 cm.
2. Prouver que les triangles CBD et BFE sont semblables.
3. Sophie affirme que l’angle 𝐵𝐹𝐸 ̂ est un angle droit. A-t-elle raison ?
4. Max affirme que l’angle 𝐴𝐶𝐷 ̂ est un angle droit. A-t-il raison ?

Correction de l’élève :

1. Dans le triangle BCD on utilise le théorème de Pythagore.
   $B{D}^2$ = $C{D}^2$ – $B{C}^2$
   $B{D}^2$ =$8,5^2$ – $7,5^2$ = 16
   Donc BD = $\sqrt{16}$ = 4 cm
2. Les triangles CBD et BFE sont semblables
   car 6,8 × 1,25 = 8,5 3,2 × 1,25 = 4 6 × 1,25 = 7,5
3. L'angle BFE ̂ est bien un angle droit car on arrive à appliquer le théorème de Pythagore dans le triangle BFE.
4. Dans BCD: C𝑜𝑠 BCD=𝐵𝐶/𝐶𝐷=7,5/8,5= BCD =28°

Max a presque raison car la somme des angles du triangle est 180° et après le calcule, ACD=89° presque 90°.

[Alef Education]

1. Je pense que la réponse 1) est correct en utilisant le théorème de Pythagore. Non?
2. Là je pense que la réponse de 2 est fausse parce deux triangles sont semblables signifie que les angles de l’un sont égaux aux angles de l’autre. Mais comment peut-on calculer les angles du trangle BEF? je comprend pas la réponse de l'élève , y a t il une autre définition des triangles semblables?

[Noemi]

@Alef-Education Bonjour,

Pour la première question, il faut préciser que le triangle $BCD$ est rectangle en $B$.
Pour la deuxième question, la propriété à préciser qui est à appliquer :
Si deux triangles sont semblables alors les longueurs des côtés homologues sont proportionnelles.