Produit scalaire exercice

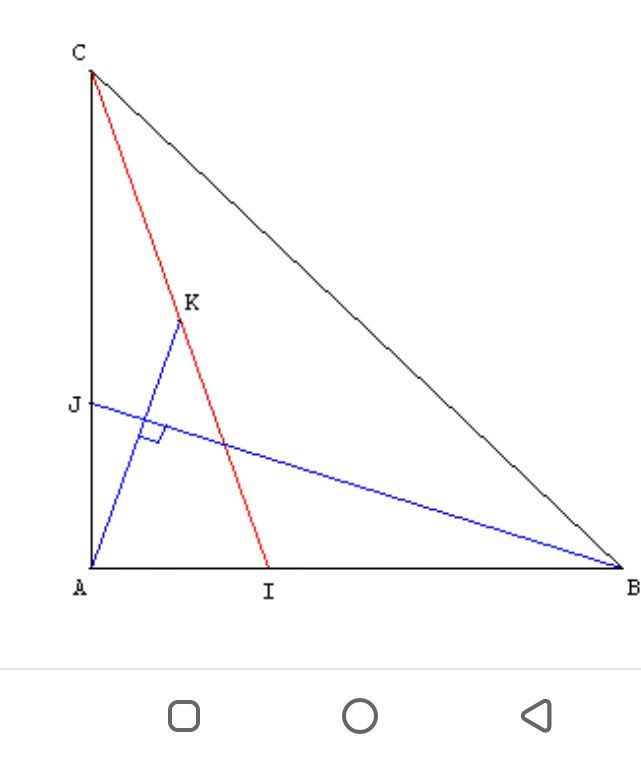
Bonjour j'ai un exercice que je comprends pas bien Soit ABC un triangle rectangle isocèle en A.
Soit I le point de [AB] tel que AI = AB/3 ;
J le point de [AC] tel que AJ = AC/3 ; et K le milieu de [IC].

Démontrer que les droites (AK) et (JB) sont perpendiculaires.

@serme Bonjour,

As-tu fait une figure ? placé un repère (avec le point A origine du repère) ?

Ce message a été supprimé !

@Noemi

@serme

Ecris les coordonnées des points $A$ , $B$ , $J$ et $K$ dans le repère $(A,AB→,AC→)(A,\overrightarrow{AB},\overrightarrow{AC})$
puis tu calcules les coordonnées des vecteurs et le produit scalaire.
Tu dois trouver : $AK→:(16;12)\overrightarrow{AK} : (\dfrac{1}{6};\dfrac{1}{2})$ et $JB→:(1;−13)\overrightarrow{JB} : (1;-\dfrac{1}{3})$

Autre méthode,
Calcule directement le produit scalaire en décomposant les vecteurs $AK→\overrightarrow{AK}$ et $JB→\overrightarrow{JB}$ .
$AK→=12(AI→+AC→)\overrightarrow{AK}=\dfrac{1}{2}(\overrightarrow{AI}+\overrightarrow{AC})$
$JB→=(JA→+AB→)\overrightarrow{JB}=(\overrightarrow{JA}+\overrightarrow{AB})$

@Noemi merci infiniment pour votre réponse j'ai compris maintenant

@serme

Parfait si tu as compris les deux méthodes.

@Noemi c'est la deuxième méthode que j'ai bien compris

@serme

La méthode directe sans passer par le repère ?

@Noemi oui

@serme

L'essentiel c'est que tu aies compris. Ce serait néanmoins bien que tu analyses la deuxième méthode.

@Noemi ok