Somme de variables aléatoires dépendantes

Bonjour,
Une urne contient 5 jetons:
3 jetons numérotés 1 et 2 jetons numérotés 2
On tire successivement sans remise 2 jetons et on note le numéro.
On note X le numéro du premier jeton et Y le numéro du deuxième jeton.
On note Z =X+Y
Déterminer E( X), E(Y) et E(Z)

La loi de X:
X : 1 ; 2
P(X) :3/5 ; 2/5
E(X)=3/5*4/5=12/25

Mais je ne vois comment établir la loi de Y car X et Y sont dépendantes.
Merci d'avance.

@kadforu Bonjour,

Pour Y, tu étudies les différentes possibilités liées au tirage du premier jeton.

Si premier jeton 1 alors deuxième jeton:
P(Y=1)=1/2, P(Y=2)=1/2
Si premier jeton 2 alors deuxième jeton:
P(Y=1)=3/4, P(Y=2)=1/4

P(y=1)=1/2 + 1/4 = 5/4 ce n'est pas possible !

@kadforu

pour $Y = 1$
La probabilité que le premier jeton soit 1 est de $35\dfrac{3}{5}$
la probabilité que le deuxième jeton soit 1 est $24\dfrac{2}{4}$
donc la probabilité du tirage $(1; 1)$ est ....

Il faut chercher ensuite la probabilité du tirage $(2; 1)$ .

Bonjour,

@kadforu , tu n'es pas obligé, mais si tu le souhaites , tu peux travailler , pour tout l'exercice, sur les couples $(x, y)$
Vu que l'on tire successivement sans remise 2 jetons parmi 5, cela fait $5×4=205\times 4=20$ éventualités (nombre d'arrangements), c'est à dire $20$ couples $(x, y)$
Je joins un tableau à 2 entrées.
$A 1, B 1, C 1$ sont les jetons numérotés 1
$D 2, E 2$ sont les jetons numérotés 2
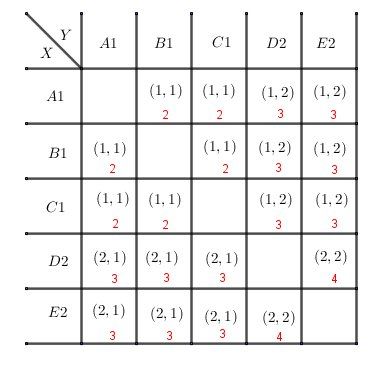
Probabilité.jpg

Les $20$ couples sont dans les cases associées (intersection ligne/colonne).
Bien sûr, la diagonale est vide vu que les tirages sont sans remise.

Pour $X = 1$ , tu comptes le nombre de couples corespondants ; Il y en a $12$
Donc $P(X=1)=1220P(X=1)=\dfrac{12}{20}$ (tu peux simplifier).
Tu trouves de la même manière $P(X=2)=880P(X=2)=\dfrac{8}{80}$ (tu peux simplifier)

Pour $Y = 1$ , tu comptes le nombre de couples corespondants : Il y en a $12$
Donc $P(Y=1)=1220P(Y=1)=\dfrac{12}{20}$ (tu peux simplifier).
Tu trouves de la même manière $P (Y = 2)$

Si tu veux avoir la loi de probabilité de $Z = X + Y$ , tu fais pareil.
Pour chaque couple, j'ai mis la somme en rouge.
$Z$ prend 3 valeurs : $2, 3, 4$
$P(Z=2)=620P(Z=2)=\dfrac{6}{20}$ (tu peux simplifier).
Tu trouves de même $P (Z = 3)$ et $P (Z = 4)$

Tu peux ensuite calculer les espérances.

Remarque : Pour E(Z), tu peux faire le calcul, mais si ton cours l'indique (?), tu peux directement utiliser la propriété : $E (X + Y) = E (X) + E (Y)$ .

Bon travail.

Merci pour vos réponses.
Je savais faire ça, avec un tableau ou un arbre.
Mais je me suis dit peut être qu'il y a moyen de calculer E(Y) directement comme dans le cas ou' X et Y sont indépendantes.

@kadforu ,
Effectivement, pour des variables non indépendantes, il n'y a pas de propriété directe, sauf pour E(X+Y)=E(X)+E(Y) valable que X et Y soient indépendantes ou non.

Bon travail .