Etude d'une fonction logarithme
-
Alef Education dernière édition par Noemi
Mon exercice 2 est le suivant:
Sur le graphique ci-dessous, on a tracé, dans le plan muni d’un repère orthonormé (O ; i ; j), la courbe représentative 𝒞 d’une fonction f définie et dérivable sur l’intervalle ]0;+∞[]0 ; +\infty[]0;+∞[.
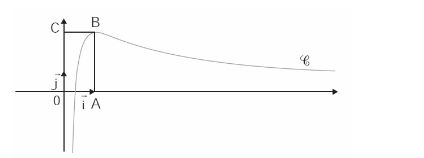
On dispose des informations suivantes :
– les points A, B, C ont pour coordonnées respectives (1 ; 0), (1 ; 2), (0 ; 2) ;
– La courbe 𝒞 passe par le point B et la droite (BC) est tangente à 𝒞 en B;
– il existe deux réels positifs a et b tels que pour tout réel strictement positif x,f(x)=a+b ln(x)xf(x)=\frac{a+b\ ln(x)}{x}f(x)=xa+b ln(x)
- a) En utilisant le graphique, donner les valeurs de f(1) et f′(1).
b) Vérifier que pour tout réel strictement positif x,
f′(x)=(b−a)−b ln(x)x2f'(x)=\frac{(b-a)-b\ ln(x)}{x^2}f′(x)=x2(b−a)−b ln(x)
c) En déduire les réels a et b. - a) Justifier que pour tout réel x appartenant à l’intervalle ]0;+∞[]0 ; +\infty[]0;+∞[ f′(x)f ′(x)f′(x) a le même signe que –ln x– ln\ x–ln x.
b) Déterminer les limites de f en 0 et en +∞+\infty+∞. On pourra remarquer que pour tout réel x strictement positif,
f(x)=2x+2ln(x)xf(x)=\frac{2}{x}+2\frac{ln(x)}{x}f(x)=x2+2xln(x)
c) En déduire le tableau de variations de la fonction f. - a) Démontrer que l’équation f(x)=1f(x) = 1f(x)=1 admet une unique solution α sur l’intervalle ]0;1]]0 ; 1]]0;1].
b) Par un raisonnement analogue, on démontre qu’il existe un unique réel β\betaβ de l’intervalle ]1;+∞[]1 ;+\infty[]1;+∞[ tel que f(β)=1f(\beta)=1f(β)=1. Déterminer l’entier nnn tel que n<β<n+1n\lt \beta \lt n+1n<β<n+1.
- a) En utilisant le graphique, donner les valeurs de f(1) et f′(1).
-
@Alef-Education Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
f(1)=...f(1)=...f(1)=...
f′(1)=...f'(1)=...f′(1)=...
-
Alef Education dernière édition par Alef Education
- a) f(1)=2f(1)=2f(1)=2 d'après les coordonnées du point CCC, et f'(1)=0$ parce que le coefficient directeur de la tangente au point B est 0. Non?
b)f′(x)f'(x)f′(x) est facile il suffit d'utiliser la formule f′g−g′fg2\frac{f'g-g'f}{g^2}g2f′g−g′f.
c) Pour déduire a et b il faut résoudre le système f(1)=2f(1)=2f(1)=2 et f′(0)=0f'(0)=0f′(0)=0, c'est à dire a=2a=2a=2 et b=a=2b=a=2b=a=2. Merci de vérifier !!! - a) Puisque b−a=0b-a=0b−a=0, $b>0$, $x^2>0$ alors f′(x)f'(x)f′(x) a le même signe que −ln(x)-ln(x)−ln(x).
b) la limite de f en +∞+\infty+∞ est 000 car 1/x1/x1/x et ln(x)/xln(x)/xln(x)/x tend vers 000 quand xxx tend vers l'infini. La limite en 000 est −∞-\infty−∞ car lnx/xlnx/xlnx/x tend vers −∞-\infty−∞ en 0+0^{+}0+.
c) Tableau de variation :
x ll 0 vers 1 vers +∞+\infty+∞
f'(x) ll + 0 -
f(x) ll −∞-\infty−∞ croissante vers 2 décroissane vers 0
- a) Une idée svp !!! (je pense c'est parcque fff est croissante de −∞-\infty−∞ vers 222 donc necessairement elle passe par le point xxx telque f(x)=1f(x)=1f(x)=1. comment puis rédiger cette question? Aussi pour la question b). Merci beaucoup pour votre aide.
- a) f(1)=2f(1)=2f(1)=2 d'après les coordonnées du point CCC, et f'(1)=0$ parce que le coefficient directeur de la tangente au point B est 0. Non?
-
Pour la question 3, tu utilises le théorème des valeurs intermédiaires.
-
Alef Education dernière édition par
@Noemi a dit dans Etude d'une fonction logarithme :
théorème des valeurs intermédiaires
TVI: Pour toute application continue f : [a, b] → ℝ et tout réel u compris entre f(a) et f(b), il existe au moins un réel c compris entre a et b tel que f(c) = u.
Puisque 1 est compris entre ]−∞,2]]-\infty,2]]−∞,2] allors il existe c∈]0,1]c\in ]0,1]c∈]0,1] tel que f(c)=1f(c)=1f(c)=1.
Puisque 1 est compris entre [0,2[ donc il existe β∈]1,+∞[\beta\in ]1,+\infty[β∈]1,+∞[ tel que f(β)=1f(\beta)=1f(β)=1. C'est bien ça?
Question: comment déterminer l’entier nnn tel que $n<\beta<n+1$ ? Merci
-
Pour chaque intervalles, il faut préciser les variations de la fonction.
Pour le calcul de β\betaβ, tu utilises la calculatrice pour en déduire une valeur approchée, puis tu détermines l'entier nnn.