Ecrire Un en fonction de n

bonsoir a tous je suis tombé sur un exercice ou je dois calculer la somme
j'ai entendu parler d'une méthode dite descendante que je ne comprend d'ailleurs pas j'aimerais un peu d'aide
la suite en question st définie par récurrence telle que
$U_{n+1}=U_n+n^2-n$ et $U_0=-2$ sachant que pour tout $n$ de $N$ $n$ > $3$ et $U_n$ > $0$

@loicstephan Bonjour,

Tu écris chaque terme
Si $n = 0$ , $U_1=U_0$
Si $n = 1$ , $U_2=U_1$
Si $n = 2$ , $U_3=U_2+2^2-2$
Si $n = 3$ , ...
.....
Pour n , $U_n=U_{n-1}+(n-1)^2-(n-1)$
Puis tu additionnes l'ensemble des égalités et tu simplifies l'expression
$U_1+U_2+...+U_n= ......$

Bonjour,

C'est sans difficultés majeures ... mais cela ne me semble quand même pas immédiat en Secondaire.

U1 = U0 + (0²-0)
U2 = U1 + (1²-1) = U0 + (0²-0) + (1²-1)
U3 = U2 + (2²-2) = U0 + (0²-0) + (1²-1) + (2²-2)
...

$\Sigma_{k=0}^{n-1} (k^2-k)$

$\Sigma_{k=0}^{n-1} (k^2) - \Sigma_{k=0}^{n-1} (k)$

On démontre (par exemple par récurrence) qu'on aboutit à :
$Un=Uo+n(n−1)(n−2)3U_n = Uo + \frac{n(n-1)(n-2)}{3}$

Et donc avec Sn = Uo + T1 + ... + Un :

$\frac{1}{3} \Sigma_{k=0}^n\ [k(k-1)(k-2)]$

$\frac{1}{3} \Sigma_{k=0}^n\ [k^3-3k^2+2k]$ (1)

Soit on sait ou on démontre par récurrence que :

$[k]=n(n+1)2\Sigma_{k=0}^n\ [k] = \frac{n(n+1)}{2}$
et
$[k2]=n(n+1)(2n+1)6\Sigma_{k=0}^n\ [k^2] = \frac{n(n+1)(2n+1)}{6}$
et
$[k3]=(Σk=0n[k])2\Sigma_{k=0}^n\ [k^3] = (\Sigma_{k=0}^n [k])^2$

Et en utilisant ces 3 relations dans (1), après simplification, on trouve :

$Sn=(n+1).Uo+n4−2n3−n2+2n12S_n = (n+1).Uo + \frac{n^4-2n^3-n^2+2n}{12}$

Si c'est quelque chose comme cela qui est attendu, cela me semble un rien "hard" en Secondaire

Peut être que la piste de Noemi permet d'attiver au but plus facilement ?

Bonjour tout le monde,

@loicstephan, tu n'a pas donné un énoncé très clair.

J'ai cru comprendre que ce que tu souhaites, c'est ce qui est écrit dans le titre "Ecrire Un en fonction de n"

Comme tu parles de "suite descendante" , je pense (?) qu'il s'agit de faite une disposition pratique "descendante", en mettant les termes de la suite les uns en dessous des autres et, ajoutant membre à membre et simplifiant, il reste $U_n$ en fonction de $n$ (personnellement, j'appelle ça une somme "télescopique")

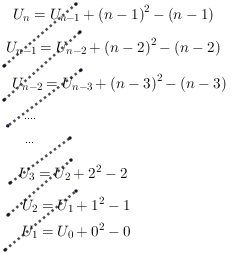
Ainsi, on obtient :

$U_n=U_0+[(n-1)^2+(n-2)^2+...+0^2]-[(n-1)+(n-2)+...+0^2]$
c'est à dire :
$Un=−2+∑k=0n−1k2−∑k=0n−1k\displaystyle U_n=-2+\sum_{k=0}^{n-1}k^2-\sum_{k=0}^{n-1}k$

Pour calculer les deux sommes $∑k=0n−1k2\displaystyle \sum_{k=0}^{n-1}k^2$ et $∑k=0n−1k\displaystyle \sum_{k=0}^{n-1}k$ , tu as les formules dans ton cours ou bien tu regardes ici, mais il faut remplacer $n$ par $n - 1$ , car les formules usuelles donnent :
$∑k=0nk2\displaystyle \sum_{k=0}^{n}k^2$ et $∑k=0nk\displaystyle \sum_{k=0}^{n}k$

http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomDemo.htm

Reposte si ce n'est pas ce que tu cherches ou si ce n'est pas clair.

bonjour @Black-Jack @mtschoon @Noemi c'est l'objet de mon post

@mtschoon @Noemi @Black-Jack
merci a tous de m'éclairer! @mtschoon c'est exactement ce que je cherchais et l'utilisation des barres en pointillé m'a permis de saisir ce qui paraissait abstrait merci bien

De rien @loicstephan,

Nous faisons au mieux.
C'est parfait si tu as bien compris les simplifications.