Produit scalaire exercice

[Traoré]

Bonjour à tous j'ai un exercice que je comprends pas
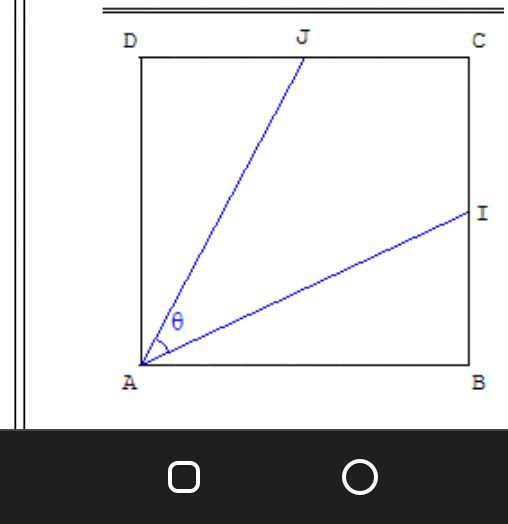
Les points I et J sont les milieux des côtés [BC] et [CD] d'un carré ABCD (où AB = a, a > 0).
On note θ l'angle (vect(AI), vect(AJ)).

Avec l'expression trigonométrique du produit scalaire, donner une valeur exacte de cos θ, puis une valeur approchée de θ en degré à 0,1° près.

[mtschoon]

@Traoré , bonjour,

Je te mets des pistes,

Tu dois exprimer $\overrightarrow{AI}.\overrightarrow{AJ}$ de deux façons différentes pour pouvoir obtenir la valeur exacte de $cos\theta$

1ère façon :
$\overrightarrow{AI}.\overrightarrow{AJ}=AI\times AJ\times cos\theta$
Avec le théorème de Pythagore dans le triangle rectangle ABI tu trouver AI ( qui est d'ailleurs égal à AJ)

2ème façon :
$\overrightarrow{AI}.\overrightarrow{AJ}=(\overrightarrow{AB}+\overrightarrow{BI}).(\overrightarrow{AD}+\overrightarrow{DJ})$
Tu développes, tu simplifies, tu calcules.

En identifiant les deux expressions de $\overrightarrow{AI}.\overrightarrow{AJ}$, sauf erreur, tu dois trouver $cos\theta =\frac{4}{5}$

Reposte si tu n'y arrives pas.

Remarque : tu pourrais aussi travailler dans un repère orthonormé, mais ça ne me semble pas être l'esprit de l'exercice.

[Traoré]

Ce message a été supprimé !

[Traoré]

@mtschoon bonsoir
Voilà ce que j'ai trouvé

1. AI.AJ=AI×AJ×Cos(AI,AJ)
   Avec le théorème de Pythagore :
   AI²=AB²+BI²=a²+(a/2)²=a²+a²/4=5a²/4
   Donc AI=AJ=a/2×√5
2. AI.AJ=(AB+BI).(AD+DJ)=AB.AD+AB.DJ+BI.AD+BI.DJ
   =0+AB×DJ+BI×AD mais je sait pas comment trouver pour le produit scalaire BI.DJ

[Noemi]

@Traoré Bonsoir,

Les vecteurs $\overrightarrow{BI}$ et $\overrightarrow{DJ}$ sont orthogonaux, donc...

[mtschoon]

Bonsoir,

@Traoré , pour le 1ere façon, tes calculs sont bons et tu dois déduire que

$\overrightarrow{AI}.\overrightarrow{AJ}=\frac{5a^2}{4}cos\theta$

Pour le 2ème façon, tu y es presque...
Comme te l'a indiqué Noemi , les vecteurs sont orthogonaux, donc
$\overrightarrow{BI}.\overrightarrow{DJ}=0$

Donc, il reste :
$\overrightarrow{AI}.\overrightarrow{AJ}=(AB\times DJ)+(BI\times AD)$

Tu calcules, sachant que $AB=AD=a$ et $DJ=BI=\frac{a}{2}$

Essaie de poursuivre et reposte si besoin.