Trigonométrie maths 1ere
-
hugo.mt_22 dernière édition par hugo.mt_22
Bonjour,
Sachant que x [1/2π ; 3/2π] et sin(x) =6/7
donnez la valeur exacte de cos(x).
-
mtschoon dernière édition par mtschoon

@hugo-mt_22 , bonjour,
Schéma :
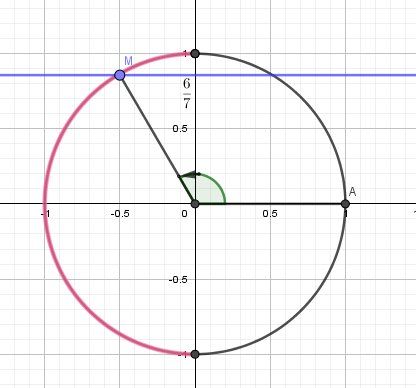
L'angle considéré est en vert sur le schéma.
IL s'agit de l'angle (OA→,OM)→(\overrightarrow{OA},\overrightarrow{OM)}(OA,OM) vu les données que tu indiques.
le cosinus cherché sera négatif (abscisse de M)Utilise la proprité usuelle : (sinx)2+(cosx)2=1(sinx)^2+(cosx)^2=1(sinx)2+(cosx)2=1
3649+(cosx)2=1\dfrac{36}{49}+(cosx)^2=14936+(cosx)2=1Tu isoles (cosx)2(cosx)^2(cosx)2 et tu déduis cosxcosxcosx
Tu peux donner ta réponse si tu veux une vérification.
-
hugo.mt_22 dernière édition par
@mtschoon Cela fait -racine carré 13/7
-
mtschoon dernière édition par

C'est bien ça.
-
Lloicstephan dernière édition par
@mtschoon a dit dans Trigonométrie maths 1ere :
C'est bien ça.
il me semble que Sin(xxx) soit compris dans l'intervalle fermé [12π;32π][\frac{1}{2π} ; \frac{3}{2π}][2π1;2π3]!!!
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
@hugo-mt_22, n'utilisant pas le Latex, écrit mal, c'est sûr, mais comme on a l'habitude, on comprend ce qu'il faut comprendre (l'intervalle que tu proposes n'a pas de sens) ; en plus, l'intervalle donné n'est pas relatif à sinxsinxsinx (comme tu l'écris) mais à xxx.
Il fallait compendre que x∈[12π,32π]x\in [\dfrac{1}{2}\pi, \dfrac{3}{2}\pi]x∈[21π,23π] (voir demi- cercle en rouge sur le schéma)